Сгибы и ритмы

Во время учебы в аспирантуре Фейнману приходилось чаще общаться с математиками, чем с физиками. Студенты, обучающиеся на двух потоках, собирались каждый полдень в общем холле на чай — опять же, дань английским традициям, — и Фейнман постоянно слышал разговоры математиков на совершенно чуждом ему профессиональном языке. Математика уже переставала развиваться как наука, непосредственно используемая в современной физике, а сами математики все больше и больше склонялись к изучению таких кажущихся непонятными разделов как, например, топология[85], рассматривающая фигуры в двух-, трех- и многомерных пространствах без учета фиксированных длин или углов. Будущие математики и физики все заметнее отдалялись друг от друга. В последний год обучения их практически ничего не связывало — ни совместные курсы, ни темы для разговоров. Фейнман же во время общих чаепитий, присоединившись к одной из групп или сидя на диване, слушал, что говорили математики о доказательствах. Так или иначе, он интуитивно чувствовал, какая теорема может быть выведена из какой леммы, даже если не понимал толком предмета спора. Ему нравились эти странные беседы. Нравилось угадывать противоречащие логике ответы на не поддающиеся наглядному представлению вопросы. Нравилось, как и всем физикам, подкалывать присутствующих, утверждая, что математики все время пытаются доказать очевидное. И хотя он подшучивал над ними, его восхищало это общество людей, увлеченных непостижимой наукой. Одним из друзей Ричарда был Артур Стоун, терпеливый молодой англичанин, обучавшийся в Принстоне на стипендию. Другим — Джон Тьюки, впоследствии ставший одним из известных в мире статистиков. Эти парни очень серьезно относились к своему свободному времени. Стоун привез из Англии блокноты, в которые можно было вставлять листы, а так как стандартная американская бумага была шире его блокнотов на два с половиной сантиметра, то у него всегда имелся большой запас бумажных полосок, из которых получались разные фигурки. Он попробовал сгибать бумагу по диагонали под углом 60° и получил ряд равносторонних треугольников. А затем, по этим сгибам, он сложил полоски в идеальный шестигранник.

Согнув полоску так, что ее края соединились, он обнаружил, что придумал необычную игрушку. Он зажал противоположные углы шестигранника и получил странную фигуру, напоминающую оригами, — новый шестигранник с другим набором треугольников. При повторном сжатии открывались другие грани. Еще один «флекс»[86] — и фигура принимала изначальный вид. В итоге получалась плоская фигурка, которую можно было выворачивать туда-сюда.

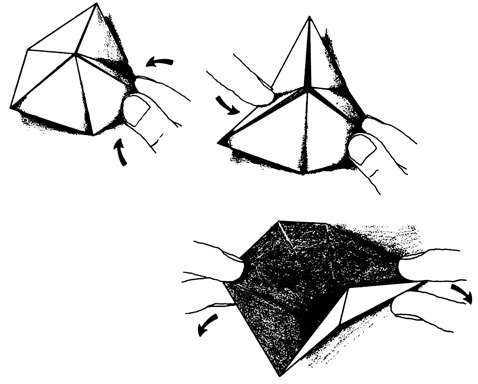
Как сделать гексафлексагон

Стоун занимался этим всю ночь, а утром взял длинную полоску и подтвердил возникшую у него гипотезу: более сложный шестигранник мог бы состоять не из трех, а из шести различных поверхностей. На этот раз цикл процесса изготовления оказался не таким простым. Три грани появлялись снова и снова, в то время как остальные три были скрыты. Нетривиальный вызов его топологическому воображению. Искусство оригами развивалось столетиями, но никому прежде не удавалось воспроизвести столь изящную фигуру. В течение нескольких дней такие флексагоны, в дальнейшем получившие названия гексафлексагоны (шесть сторон, шесть поверхностей), циркулировали по обеденному залу во время обедов и ужинов. А затем появилась Комиссия по изучению флексагонов, в состав которой вошли Стоун, Тьюки, математик Брайант Такерман и их друг физик Фейнман. Оттачивая свое мастерство и ловкость в обращении с листами и полосками бумаги, они сделали гексафлексагоны с двенадцатью поверхностями, скрытыми внутри, потом с двадцатью четырьмя и даже с сорока восьмью. Количество вариаций в каждом виде флексагонов стремительно увеличивалось в соответствии с далеко не очевидным законом. Теория флексагонов развивалась, занимая свое место на стыке топологии и теории сетей. Фейнман же внес в нее свой вклад, придумав диаграмму, впоследствии названную в его честь, которая показывала все возможные конфигурации гексафлексагона.

Семнадцать лет спустя, в 1956 году, в журнале Scientific American будет опубликована статья Мартина Гарднера «Флексагоны» (Flexagons), которая даст старт его карьере как человека, способствовавшего развитию занимательной математики. За двадцать пять лет ведения колонки «Математические игры» он издал более сорока книг. Первая же его статья вызвала настоящий бум у детей. В форме флексагонов изготавливали рекламные флайеры и открытки. Они вдохновили на написание нескольких книг и статей для учащихся младшей и средней школы. Среди сотен писем, пришедших в редакцию, находилось и послание из лаборатории Аллена дю Монта из Нью-Джерси. Оно начиналось так:

«Дорогая редакция, меня очень заинтересовала статья “Флексагоны”, опубликованная в вашем декабрьском номере. Нам потребовалось всего шесть или семь часов, чтобы склеить гексафлексагон для получения нужной фигуры. И с тех пор он не перестает привлекать внимание. Но у нас тут вот какая проблема. Сегодня утром, когда один из сотрудников сворачивал гексафлексагон, кончик его галстука попал между граней. И с каждым следующим сгибом галстук все больше и больше исчезал в фигуре. После шести сгибов он полностью пропал там. Нам безумно нравится изготавливать фигуры, и мы не смогли проследить, как все получилось, но мы нашли шестнадцатую конфигурацию гексафлексагона…»

Игровой настрой и жажда интеллектуальных исследований шли теперь рука об руку. Целые дни Фейнман проводил, сидя на подоконнике в своей комнате, и с помощью бумажных полосок переправлял муравьев к упаковке сахара, подвешенной на веревках. Ему хотелось выяснить, как муравьи общаются между собой и способны ли они воспринимать геометрические образы. Однажды зимой, когда он, как обычно, сидел у окна, один из соседей ворвался к нему в комнату, держа в руках горшочек с «Джелло»[87], распахнул окно, продолжая рьяно помешивать желе в банке, и закричал: «Не мешай мне!» Он пытался установить, как будет застывать желе, когда его перемешивают. Другой студент затеял спор о способностях передвижения человеческих сперматозоидов. Фейнман исчез и вернулся вскоре с готовым образцом. Вместе с Джоном Тьюки Ричард долгое время изучал способность людей контролировать время с помощью счета. Он бегал вверх и вниз по лестнице, чтобы увеличить частоту сердцебиений, и одновременно считал удары сердца и вел отсчет секундам. Они обнаружили, что Фейнман мог одновременно считать про себя и следить за временем, но если начинал говорить, то терял счет минутам. Тьюки же мог вести отсчет времени, декламируя вслух стихи. Они предположили, что, когда дело касалось счета, их мозг задействовал различные функции. Фейнман использовал акустический ритм, слушая числа, а Тьюки представлял что-то вроде ленты с написанными на ней цифрами, проносящимися перед глазами. Годы спустя Тьюки говорил: «Нас интересовал собственный опыт. Мы получали удовольствие от того, что испытывали, и сводили всё к простым вещам, которые могли наблюдать».

Порой что-то, лежащее за пределами научных знаний, привлекало внимание Фейнмана и буквально приставало к нему, как колючка от каштана. Один из студентов увлекся поэзией Эдит Ситуэлл, в то время считавшейся довольно эксцентричной из-за используемых ею вычурных сочетаний звуков и какофонии стихов, напоминавшей джазовые ритмы. Молодой человек продекламировал несколько стихотворений вслух, и внезапно Фейнман что-то уловил. Он взял книгу и принялся восторженно читать.

«Ритм — один из основных проводников между сном и реальностью, — говорила автор о собственных стихах. — В мире звуков ритм — то же самое, что свет в мире визуальных образов». Для Фейнмана ритм был и наркотиком, и инструментом. Его мысли иногда плавно перетекали и двигались, словно под удары барабана. Друзья замечали это, когда он начинал выбивать пальцами такт по столу или тетрадям. Ситуэлл писала:

Вселенная расцветает в моей голове,

Я живу наяву, но словно во сне.

Мысли о мире и мысли о дне,

О том, что все возможно, приходят ко мне.