Что нам известно о гравитации и свете?

Гравитация – наиболее знакомая нам из четырех сил. Мы все еще в раннем детстве узнаем, что когда мороженое шлепается на пол или сам ты падаешь с качелей, винить следует гравитацию. Если обычного человека спросить, сильна гравитация или же слаба, он, скорее всего, скажет: “Очень сильна”, – и ошибется. Из четырех сил, действующих во вселенной, эта – самая слабая. Однако в повседневной жизни мы наглядно видим действие совокупных сил притяжения всех частиц, составляющих нашу немаленькую планету. Вклад каждой отдельной частицы в эту общую силу бесконечно мал. Чтобы замерить еле заметное притяжение между какими-либо двумя небольшими объектами, требуется чрезвычайно чувствительная аппаратура. Но поскольку под действием гравитации предметы не отталкиваются, а притягиваются друг к другу, эти силы складываются.

Физик Джон Уилер изображал гравитацию как своего рода вселенскую демократию: каждая частица имеет “голос”, которым может воздействовать на все остальные частицы. Когда частицы собираются вместе и голосуют блоком (это может быть звезда или планета, как наша Земля), их влияние заметно возрастает. Соединяясь в таких крупных телах, как Земля, слабые гравитационные взаимодействия отдельных частиц становятся существенной силой – влиятельной политической партией.

Чем больше материальных частиц составляет какое-либо тело, тем больше масса этого тела. Масса и размер – не одно и то же. Говоря о массе тела, мы имеем в виду количество вещества в нем (число избирателей в данном блоке) и степень устойчивости этого тела к попыткам изменить скорость и направление его движения. А насколько плотно или свободно упакованы в нем частицы, не важно.

Сэр Исаак Ньютон, Лукасовский профессор математики (он занимал в Кембридже в XVII веке ту же должность, которую в 1980 году получил Хокинг), описал закон всемирного тяготения применительно к более-менее стандартным ситуациям. Согласно теории Ньютона, тела во вселенной не находятся в покое. Прежде считалось, будто тела находятся в покое до тех пор, пока внешняя сила не толкнет их или не потянет, а когда это воздействие “исчерпается”, они снова приходят в состояние покоя. На самом же деле, если на тело не воздействует никакая сила, оно продолжает двигаться по прямой, не изменяя скорости, и правильнее представлять все объекты во вселенной в постоянном движении. Мы можем измерить скорость или направление своего движения относительно других тел во вселенной, но мы не можем сравнить свою скорость с абсолютным покоем или установить абсолютные координаты, неизменный север, восток, запад и юг.

Например, если бы Луна была одинока во вселенной, она бы не пребывала в покое, но двигалась бы по прямой без ускорения. (Разумеется, если б не существовало ничего, кроме Луны, не было бы возможности установить сам факт ее движения, привязать его к каким-то ориентирам.) Но Луна не одинока. Сила всемирного тяготения воздействует на нее, вынуждая менять скорость и направление. Откуда взялась эта сила? От сплоченного блока избирателей, то бишь от массивного объекта под названием Земля. Луна противится навязываемым переменам. Она старается сохранить движение по прямой. Сила сопротивления зависит от количества избирателей в составе Луны, от ее массы. И в свою очередь, притяжение Луны воздействует на Землю. Самое очевидное проявление этого – приливы.

Согласно законам Ньютона, сила притяжения между двумя телами зависит от массы этих тел. При прочих равных чем больше масса, тем больше и притяжение. Если бы масса Земли была вдвое больше, соответственно возросло бы и притяжение. Любое изменение массы Луны или Земли отразится на притяжении между ними. Ньютон также обнаружил, что притяжение становится слабее, если два тела отдаляются друг от друга. Если бы Луна оказалась на вдвое большем расстоянии от Земли, чем теперь, притяжение между Луной и Землей стало бы вчетверо слабее. Обычно это формулируется следующим образом: сила взаимного притяжения двух тел прямо пропорциональна их массе и обратно пропорциональна квадрату расстояния между ними.

Созданная Ньютоном теория всемирного тяготения имела редкий для научной гипотезы успех: более двухсот лет ее даже не пытались корректировать. Мы до сих пор пользуемся этой теорией, хотя и знаем, что в определенных ситуациях она перестает быть истинной, например, когда гравитация чрезвычайно возрастает (в окрестностях черных дыр) или когда тела движутся со скоростью, близкой к скорости света.

Изъяны в теории Ньютона первым разглядел на заре ХХ века Альберт Эйнштейн. Если сила взаимного притяжения двух тел как-то связана с расстоянием между ними, то достаточно отодвинуть Солнце от Земли, и гравитационное взаимодействие этих двух тел мгновенно изменится. Но так ли это?

Разработанная Эйнштейном специальная теория относительности предполагает, что скорость света остается одинаковой независимо от нашего местоположения во вселенной и нашего собственного движения, причем ни одно тело не может двигаться со скоростью, превышающей скорость света. Свет Солнца достигает Земли примерно через восемь минут, то есть мы всегда видим Солнце таким, каким оно было восемь минут назад. Значит, если Солнце отодвинется от Земли, Земля еще восемь минут не будет замечать этого и не почувствует никаких последствий этой глобальной перемены. Наша планета еще восемь минут будет двигаться по прежней орбите, как будто ничего не произошло. Иными словами, взаимное притяжение двух тел не может измениться в мгновение ока, потому что гравитация распространяется не быстрее скорости света. Информация о местонахождении Солнца не может мгновенно пересечь космическое пространство. Максимально возможная скорость – 300 000 км/сек.

Из этого следует, что, говоря о телах, движущихся во вселенной, нельзя ограничиться лишь тремя измерениями пространства. Поскольку информация не может распространяться быстрее скорости света, тела, которые находятся на астрономических расстояниях, не существуют для нас или друг для друга без учета фактора времени. Описывать вселенную в трех измерениях так же плоско, как сводить к двум измерениям куб. Нужно признать наличие четырех измерений, учесть координату времени и говорить не о пространстве, но о пространстве-времени.

Эйнштейну понадобилось несколько лет, чтобы привести теорию гравитации в соответствие с его открытиями о свете и движении на скорости, близкой к скорости света. В 1915 году он обнародовал общую теорию относительности, которая предлагает нам рассматривать гравитацию не как силу, действующую между телами, а как форму, кривую четырехмерного пространства-времени. В общей теории относительности гравитация – это геометрия вселенной.

Брайс Девитт из Техасского университета советовал приучать себя к мысли об этой кривой, представляя себе человека, верящего, что Земля плоская, и старающегося начертить на ней решетку:

Результат можно в ясный день наблюдать с высоты птичьего полета над возделанными регионами Великих равнин. Дороги, проложенные с севера на юг и с запада на восток, делят поля на квадратные мили. Восточно-западные дороги тянутся непрерывно милю за милей, но дороги с севера на юг время от времени дают уклон к востоку или к западу. Эти зигзаги подсказывает изгиб земного шара, без них дороги начали бы сходиться, и площадь очередного участка не дотянула бы до квадратной мили. В трехмерном мире представим себе строительство гигантской лестницы – вроде бы несложно соединять перекладины равной длины под углом 90 и 180 градусов. Будь пространство плоским, строительство можно было бы продолжать до бесконечности, однако если пространство искривлено, придется укорачивать и растягивать перекладины, иначе они не совпадут[93].

Эйнштейн считал, что искривление вызвано присутствием массы или энергии. Любое крупное тело усиливает искривление пространства-времени. Все, что движется “по прямой”, вынуждено сворачивать на этот кривой путь. Представьте себе батут (рис. 5.1). В центре лежит шар для боулинга, резиновая основа под ним прогибается. Попытайтесь прокатить мяч для гольфа строго по прямой мимо мяча для боулинга. Мяч для гольфа непременно отклонится от своего маршрута, попав в углубление, продавленное мячом для боулинга. Более того: возможно, мяч для гольфа даже опишет эллипс и покатится обратно к вам. Что-то в том же роде происходит, когда Луна пытается двигаться по прямой мимо Земли. Земля продавливает пространство-время, как мяч для боулинга продавливает батут. Лунная орбита максимально приближена к прямой в параметрах искривленного пространства-времени.

Эйнштейн описывал то же явление, которое наблюдал Ньютон. В теории Эйнштейна массивный объект продавливает пространство-время. Ньютон считал, что массивный объект излучает некую силу. Результат в обоих случаях один и тот же: второй объект изменяет направление движения. В общей теории относительности “гравитационное поле” и “искривление пространства-времени” – синонимы.

Рассчитывая орбиты планет Солнечной системы по Ньютону и по Эйнштейну, вы получите практически одинаковые результаты, за исключением лишь расчетов для Меркурия. Поскольку Меркурий ближе других планет находится к Солнцу, он более подвержен его притяжению. Теория Эйнштейна предсказывает несколько иные последствия такого положения Меркурия, нежели теория Ньютона, и астрономические наблюдения подтвердили, что Эйнштейн точнее, чем Ньютон, описал движение Меркурия.

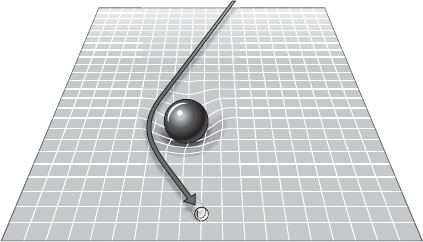
Рис. 5.1. Шар для боулинга продавливает резиновый батут, на котором он лежит. При попытке прокатить мимо шара для боулинга другой мячик, поменьше, этот мячик отклоняется от прямого пути там, где попадает во вмятину от шара для боулинга. Так и в пространстве-времени траектория объектов искривляется под действием более массивных объектов.

Теория Эйнштейна предполагает, что искривлению пространства-времени подвластны и другие объекты помимо лун и планет. По кривой движутся и частицы света – фотоны. Когда луч далекой звезды проходит неподалеку от Солнца, искривление пространства-времени возле Солнца слегка отклоняет этот луч от прямой в сторону нашего светила, подобно тому как мячик для гольфа в нашем эксперименте отклонялся ближе к шару для боулинга. Возможно, отклонившись от прямого пути, этот луч в итоге достигнет Земли. Солнце светит настолько ярко, что разглядеть свет далеких звезд мы можем лишь во время затмения. Но если во время затмения мы увидим такой луч, то, не зная, как воздействовало на него притяжение Солнца, мы составим ложное представление о том, в каком направлении двигался луч света и где находится та звезда (рис. 5.2). Астрономы используют это явление: они измеряют массу небесных тел, основываясь на том, как сильно те искажают лучи далеких звезд. Чем больше масса “искривителя”, тем сильнее искривление.

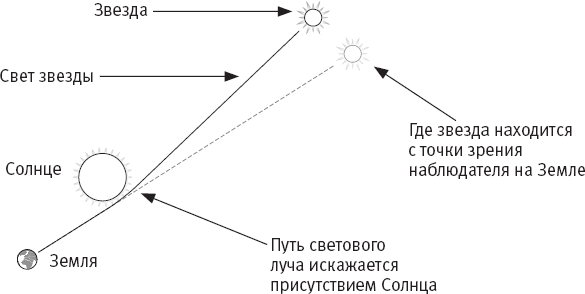
Рис. 5.2. Поскольку присутствие большой массы вызывает искривление пространства-времени, свет далекой звезды отклоняется от прямой, проходя рядом с таким массивным телом, как Солнце. Отметьте разницу между видимой с Земли позицией звезды и ее реальным положением.

До сих пор мы обсуждали гравитацию в макромасштабах. Именно в таких масштабах она становится очевидна – когда действует на уровне звезд, галактик, целой вселенной, – и с этим масштабом Хокинг имел дело под конец 1960-х. Однако – вспомним главу 2 – гравитацию можно рассматривать и на самом микроскопическом, квантовом уровне. Более того, пока мы не изучим гравитацию на квантовом уровне, мы не сможем соотнести ее с тремя другими силами, две из которых только на этом уровне и действуют. При квантово-механическом описании гравитационных взаимодействий Земли и Луны предполагается обмен гравитонами (разновидностью бозонов, частиц-вестников гравитационной силы) между теми частицами, из которых состоят эти два небесных тела.

Нарисовав фон, побалуем себя страничкой научной фантастики.