Побег из черной дыры?

Свою идею – горизонт событий черной дыры никогда не сокращается – Стивен Хокинг впервые представил научному сообществу в декабре 1970 года на Симпозиуме по астрофизике и теории относительности в Техасе[103]. Тогда он оговорился, что при всем сходстве формулировок – неубывание области горизонта событий, неубывание энтропии – это всего лишь аналогия.

Еще один принстонский выученик Уилера, Яков (Джейкоб) Бекенштейн, не согласился с такой оговоркой. Он решил, что горизонт событий черной дыры не только похож по своим свойствам на энтропию – он и есть энтропия[104]. Измеряя радиус горизонта событий, мы тем самым измеряем энтропию черной дыры. Бросив ящик в черную дыру, мы не уничтожим энтропию внутри черного ящика – энтропия присутствует и внутри черной дыры, и мы лишь увеличим ее. Упав в черную дыру, наш ящик с молекулами внутри приплюсуется к общей массе черной дыры, и соответственно увеличится горизонт событий. Вместе с тем возрастет и энтропия.

Но тут возникает затруднение. Нарастание энтропии означает повышение температуры. Объект, которому присуща энтропия, не может быть совершенно холодным, а если у него есть температура, объект должен излучать энергию. Раз излучается энергия, мы уже не вправе говорить, что “оттуда” ничего не исходит. Но ведь из черной дыры ничего не должно исходить.

Хокинг счел гипотезу Бекенштейна ошибочной и даже сердился, что Бекенштейн, мол, исказил его открытие о неубывании горизонта событий. В 1972 и 1973 годах вместе с двумя другими физиками, Джеймсом Бардином и Брэндоном Картером, он, казалось бы, двигался навстречу этой гипотезе, разработав в итоге целых четыре закона механики черной дыры, практически совпадающих с четырьмя хорошо известными законами термодинамики, – нужно лишь заменить выражение “горизонт событий” на термин “энтропия”, а вместо “сила притяжения на поверхности горизонта” писать “температура”[105]. Тем не менее три соавтора продолжали настаивать, что это всего лишь аналогия, и в окончательной версии своей статьи[106] подчеркивали, что четыре закона механики черной дыры хотя и похожи на законы термодинамики, но отнюдь с ними не совпадают. Сколько бы мы ни проводили параллелей между свойствами энтропии и областью внутри горизонта событий, в черной дыре энтропии нет, писали они, поскольку из нее ничего не исходит. Такой аргумент Бекенштейну крыть было нечем, и все же, хотя он был в ту пору аспирантом, а эти трое уже сделали себе имя в науке, Бекенштейн не сдавался. В итоге выяснилось, что ошибались Хокинг, Бардин и Картер. Сам же Хокинг и доказал это.

В 1962 году, когда Хокинг поступил в Кембридж, он предпочел космологию, науку о бесконечно больших, квантовой механике, науке о бесконечно малых. Теперь, в 1973 году, он решил сменить угол зрения и изучить черные дыры как раз с точки зрения квантовой механики. Впервые кто-то всерьез – и с успехом – попытался объединить две главные физические теории ХХ века, теорию относительности и квантовую механику. Как мы знаем из главы 2, несводимость этих теорий стала главным препятствием на пути к созданию теории всего.

В январе 1973 года Хокингу исполнился 31 год. Новый год принес ему публикацию его первой книги, написанной в соавторстве с Джорджем Эллисом и посвященной Деннису Сиаме. Эту работу, “Крупномасштабная структура пространства-времени”, Хокинг теперь считает “крайне специальной и едва ли читабельной”[107]. Книгу до сих пор можно отыскать на полках академических книжных магазинов, и любой читатель, кроме специалиста по физике, пожалуй, согласится с таким суждением автора, если попытается ее пролистать. Бестселлером, подобным “Краткой истории времени”, этой работе не стать, но в своей области она признана классической.

В августе и сентябре того же года, в длинные университетские каникулы, Хокинги съездили в Варшаву на празднование пятисотлетия со дня рождения Николая Коперника, а оттуда дальше на восток, в Москву. Они пригласили в эту поездку и Кипа Торна, поскольку тот уже пять лет сотрудничал с советскими физиками и знал ходы и выходы в Союзе. Хокинг хотел потолковать с Яковом Борисовичем Зельдовичем и его аспирантом Александром Старобинским. Эти двое советских ученых сумели доказать, что принцип неопределенности подразумевает: вращаясь, черная дыра создает и испускает частицы, порожденные энергией вращения. Излучение не выходит за пределы горизонта событий, оно притягивается обратно и замедляет вращение черной дыры, пока вращение вовсе не остановится, а вместе с вращением прекратится и излучение. Хокинг заинтересовался идеями Зельдовича и Старобинского, однако их вычисления его не устраивали. После этой встречи он вернулся в Кембридж с твердым намерением отыскать математическое решение получше.

Хокинг ожидал, что его подсчеты подтвердят: черная дыра испускает то самое излучение, которое предсказывали русские, однако он открыл нечто куда более поразительное: “К собственному изумлению, я обнаружил, что даже невращающиеся черные дыры должны с постоянной интенсивностью порождать и испускать частицы”[108]. Сперва Хокинг заподозрил собственные вычисления и много времени провел в поисках ошибки. В особенности он не хотел, чтобы о таком повороте событий прознал Бекенштейн, ведь выходило, что тот был прав, отождествляя площадь горизонта событий и энтропию. Однако чем дольше Хокинг размышлял об этом, тем очевиднее становилось, что его вычисления вполне соответствуют истине. И вот что интересно: спектр испускаемых частиц как раз соответствовал излучению любого объекта с повышенной температурой.

Бекенштейн, выходит, был прав: нет смысла бросать вещество в черные дыры, словно в огромные урны, – энтропия от этого не уменьшится и порядка во вселенной не прибавится. Вещество, обладающее энтропией, провалится в черную дыру, площадь горизонта событий увеличится, энтропия черной дыры возрастет. Суммарная энтропия вселенной внутри черной дыры и за ее пределами никак не уменьшится.

Однако Хокингу предстояло расправиться с загадкой посложнее: как может черная дыра быть горячей и испускать частицы, если ничто не выходит за пределы горизонта событий? Ответ он нашел в квантовой механике.

Рассуждать о пространстве как о вакууме не вполне правильно, ведь пространство, как мы уже убедились, не бывает совершенно пустым. Сейчас мы поймем, почему это так.

Принцип неопределенности гласит: нам не дано точно знать и положение частицы, и ее количество движения одновременно в любой момент времени. И более того, мы не можем точно знать величину поля и скорость его изменения во времени. Чем точнее мы знаем величину поля, тем менее точно знаем скорость изменения, и наоборот – вечные качели. Зато величина поля никогда не бывает равна нулю: ноль – самое что ни на есть точное измерение как величины, так и скорости изменения, а принцип неопределенности не допускает такой точности измерения. В абсолютно пустом пространстве величина любого поля должна быть равна нулю. Нет нулевой величины поля – нет и пустого пространства.

Вместо пустого пространства, полного вакуума, которое мерещится “где-то там” большинству из нас, приходится иметь дело с минимальной неточностью, с некоторой неопределенностью насчет того, какова же величина поля в “пустом” пространстве. Вот один из способов постичь колебания величины этого поля, чуточку больше нуля – чуточку больше, но никогда не ровно ноль.

Постоянно возникают пары частиц – например, фотонов или гравитонов. Сперва пара держится вместе, затем распадается. Спустя невообразимо короткий промежуток времени эти частицы вновь соединяются, и происходит аннигиляция – частицы взаимно уничтожают друг друга. Квантовая механика учит, что такие события происходят все время и повсюду в так называемом “вакууме”. Возможно, эти частицы не “реальны”, то есть мы не сумеем зарегистрировать их с помощью приборов, но они и не плод воображения. Даже если эти частицы всего лишь “виртуальны”, мы знаем об их существовании, поскольку можем замерить их влияние на другие частицы.

Некоторые пары состоят из частиц материи, фермионов. В таком случае одна из частиц в паре принадлежит к антиматерии. Антиматерия, с которой нас познакомили научно-фантастические романы, видеоигры и фильмы (она служит топливом кораблю “Энтерпрайз”), не вымысел.

Вероятно, вы слышали о том, что общее количество энергии во вселенной всегда остается постоянным. Энергия не может вдруг взяться из ниоткуда. Как же применить этот закон к постоянно образующимся парам частиц? Они-то ведь порождаются “взятой взаймы” на очень краткое время энергией. Постоянного изменения не происходит. Одна частица в паре несет отрицательную энергию, другая – положительную. Вместе они уравновешивают друг друга. Общее количество энергии во вселенной не увеличивается.

Хокинг рассуждал так: на горизонте событий черной дыры появляется множество таких пар. Он представлял себе, как возникает пара виртуальных частиц. Прежде чем разошедшиеся частицы встретятся вновь и аннигилируют, одна из них, та, что с отрицательной энергией, пересечет горизонт событий и попадет внутрь черной дыры. Означает ли это, что и положительно заряженная частица должна последовать за своей неудачливой напарницей, разыскать ее и вместе с ней погибнуть? Нет. Гравитационное поле на горизонте событий черной дыры настолько сильно, что способно творить чудеса с “виртуальными” частицами, даже с теми, кому не повезло получить отрицательную энергию: оно превращает их из “виртуальных” частиц в “реальные”.

Это превращение радикально изменяет судьбу частиц. Им уже нет необходимости разыскивать друг друга, чтобы аннигилировать. Они смогут существовать по отдельности, причем намного дольше. Разумеется, и частица с положительной энергией может упасть в черную дыру, но может и не упасть. Она освобождается от уз партнерства. Она может спастись бегством. Наблюдателю из удаленной точки покажется, будто она вылетела изнутри черной дыры. На самом деле эта частица находилась точно на наружной границе. А вторая частица из пары унесла отрицательную энергию внутрь черной дыры (рис. 6.2).

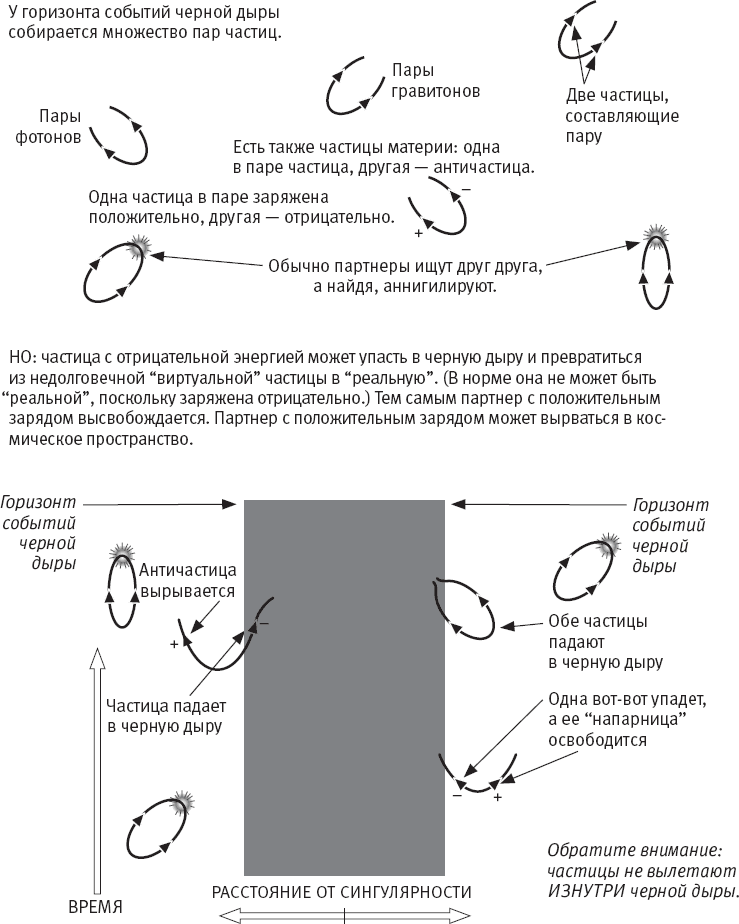
Рис. 6.2. Излучение Хокинга.

Теперь такого рода излучение черных дыр называется излучением Хокинга. И, сделав второе свое великое открытие о природе черных дыр, Хокинг сам и доказал, что первое его прославленное открытие, второй закон динамики черных дыр (площадь горизонта событий никогда не сокращается), не всегда верно. Излучение Хокинга может привести к тому, что черная дыра начнет уменьшаться в размерах и в конечном итоге вовсе испарится. Это было уже не просто открытие – революция.

Почему излучение Хокинга приводит к уменьшению размеров черной дыры? Превращая “виртуальные” частицы в “реальные”, черная дыра теряет энергию. Как это возможно, если ничто не выходит за пределы горизонта событий? Как может черная дыра что-то “терять”? Ответ хитроумный: попадая в черную дыру, частица с отрицательной энергией приносит в черную дыру именно отрицательную энергию, то есть общее количество энергии в черной дыре убывает. Добавить отрицательную энергию значит вычесть энергию.

Так излучение Хокинга “грабит” черную дыру, отнимая у нее энергию. С убыванием энергии автоматически убывает и масса. Вспомните уравнение Эйнштейна Е=mc². Е – энергия, m – масса, с – скорость света. Когда в левой части уравнения убывает энергия (именно это происходит в рассмотренном случае в черной дыре), должно убывать и произведение в правой части уравнения. Скорость света – с – константа. Следовательно, убывает масса. Итак, предположив, что черная дыра теряет энергию, мы допускаем также, что в ней убывает и масса.

Учтем это и вспомним открытие Ньютона, формулу гравитации: если изменяется масса тела, то непременно меняется и сила притяжения, с какой это тело воздействует на другие тела. Если уменьшится масса Земли (на этот раз мы говорим о массе, а не о размерах), ее гравитационное поле на орбите Луны окажется слабее. Если черная дыра потеряет часть своей массы, сила ее притяжения на горизонте событий (границе невозврата) станет меньше. Тогда и вторая космическая скорость на таком расстоянии от черной дыры станет меньше скорости света. Значит, равенство “вторая космическая скорость = скорость света” будет действительно для меньшего, чем прежде, радиуса. Появится новый горизонт событий – ближе к черной дыре. Площадь горизонта событий сократится. Только так мы можем объяснить уменьшение размеров черной дыры.

Если замерить излучение Хокинга из большой черной дыры, возникшей в результате коллапса звезды, то мы будем разочарованы: такая огромная черная дыра, а температура на поверхности лишь на миллионную долю градуса превышает абсолютный ноль. И чем больше черная дыра, тем ниже ее температура. Хокинг утверждает: “Черная дыра с десятикратной солярной массой может испускать несколько тысяч фотонов в секунду, но их длина волны совпадает с размерами черной дыры, а энергии так мало, что мы не сумеем их обнаружить”[109]. Ведь чем больше масса черной дыры, тем больше и площадь горизонта событий. Чем больше площадь горизонта событий, тем выше энтропия. Чем выше энтропия, тем ниже температура поверхности и уровень излучения.