От теоремы Пифагора до Великой теоремы Ферма

От теоремы Пифагора до Великой теоремы Ферма

О теореме Пифагора и бесконечном числе пифагоровых троек шла речь в книге Э.Т. Белла «Великая проблема» — той самой библиотечной книге, которая привлекла внимание Эндрю Уайлса. И хотя пифагорейцы достигли почти полного понимания пифагорейских троек, Уайлс скоро обнаружил, что у невинного на первый взгляд уравнения x² + y² = z² имеется и темная сторона — в книге Белла давалось описание математического чудовища.

В уравнение Пифагора входят три числа x, y и z, все три числа входят в квадрате (например, x² = x·x):

x² + y² = z²

Но в той же книге Белла приводилось и уравнение, очень похожее на уравнение Пифагора, но отличающееся от него тем, что все числа входят в кубе (например, x³ = x·x·x). Так называемая степень переменной x в этом уравнении равна не 2, а 3:

x³ + y³ = z³

Найти целочисленные решения уравнения Пифагора, т. е. пифагоровы тройки, было сравнительно легко, но стоит лишь степени измениться с 2 на 3 (т. е. заменить квадраты кубами), как решение уравнения, столь похожего на уравнения Пифагора, в целых числах, по-видимому, становится невозможным. Поколения математиков исписывали страницу за страницей в своих блокнотах в тщетной надежде найти решение уравнения в целых числах.

При решении исходного «квадратного» уравнения плитки, из которых состояли два квадрата, требовалось расположить так, чтобы они образовывали третий квадрат более крупных размеров. В случае решения «кубического» уравнения из кубиков, образующих два куба, требуется составить третий куб более крупных размеров. Ясно, что независимо от того, какие два куба выбраны в качестве исходного, из образующих их кубиков можно сложить либо третий куб, причем несколько кубиков останутся «лишними», либо неполный (недостроенный) куб. Ближайшим к идеальному кубу будет такая кладка, в которой один кубик останется лишним или окажется недостающим. Например, если мы начнем с кубов 63 и 83 то, рассыпав их на кубики, сможем сложим из них кладку, в которой всего лишь одного кубика не хватит до полного куба 93 (рис. 5).

+

=

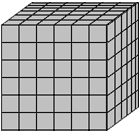
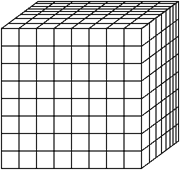
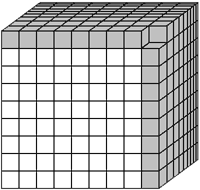
6³ + 8³ = 9³ - 1

216 + 512 = 729 - 1

Рис. 5

Найти три целых числа, которые в точности удовлетворяют кубическому уравнению, по-видимому, невозможно. Иначе говоря, по-видимому, у уравнения

x³ + y³ = z³

не существует целочисленных решений. Более того, если степень повысить с 3 (куба) до любого большего целого числа (т. е. до 4, 5, 6…), то найти целочисленное решение такого уравнения, по-видимому, также невозможно. Иначе говоря, у более общего уравнения

xⁿ + yⁿ = zⁿ,

где n больше 2, решения в целых числах не существует. Всего лишь изменив 2 в уравнении Пифагора на любое целое число б?льшее 2, мы вместо сравнительно легко решаемого уравнения получаем задачу умопомрачительной сложности. Великий математик XVII века француз Пьер де Ферма сделал удивительное заключение: он утверждал, что знает, почему никому не удавалось найти решение общего уравнения в целых числах. По его словам, причина заключалась в том, что такого решения не существует.

Ферма был одним из наиболее блестящих и загадочных математиков в истории. Как и всякий другой, он не мог проверить бесконечно много чисел, но был абсолютно уверен в том, что не существует тройки целых чисел, которая удовлетворяла бы общему уравнению, так как его уверенность опиралась на доказательство. Подобно Пифагору, которому вовсе не требовалось проверить все мыслимые треугольники, чтобы убедиться в правильности своей теоремы, у Ферма не было необходимости перепробовать все мыслимые тройки целых чисел, чтобы убедиться в справедливости его теоремы.

Прочитав всю книгу Э.Т. Белла от корки до корки, Уайлс узнал, как Ферма был восхищен теоремой Пифагора и ее доказательством, и как сам постепенно увлекся изучением «испорченного» уравнения Пифагора. Прочитав о том, как Ферма провозгласил, что даже если математики всего мира потратят целую вечность, чтобы найти решение уравнения, носящего ныне его имя, в целых числах, то и тогда им не удастся найти ни одного решения. Уайлс в нетерпении перевернул несколько страниц, предвкушая удовольствие от разбора доказательства Великой теоремы Ферма, но тщетно: доказательства не было. Не было его не только в книге Э.Т. Белла, но и нигде. В конце книги говорилось, что найденное Ферма доказательство давно утеряно. Никаких указаний, намеков или догадок относительно того, как можно было бы восстановить доказательство или построить его заново не было. Уайлс был заинтригован, разъярен и озадачен. По крайней мере, он находился в хорошей компании.

Более 300 лет многие из крупнейших математиков пытались вновь открыть утерянное доказательство Ферма, но тщетно. С неудачей очередного поколения следующее поколение испытывало все большее разочарование и решимость. В 1742 году, почти через сто лет после смерти Ферма, швейцарский математик Леонард Эйлер обратился к своему другу Клеро с просьбой поискать в доме Ферма, не осталось ли где-нибудь клочка бумаги с жизненно важным фрагментом доказательства. Но никому никогда не удалось найти ни малейшего намека относительно того, каким могло быть доказательство Ферма. В гл. 2 мы узнаем более подробно о загадочной фигуре Пьера де Ферма, и о том, как было утеряно доказательство. А пока мы ограничимся лишь тем, что скажем: Великая теорема Ферма, проблема, над решением которой математики ломали головы на протяжении столетий, захватила воображение юного Эндрю Уайлса.

Десятилетний мальчик в библиотеке на Милтон-роуд не мог оторвать взгляда от самой знаменитой проблемы математики. Обычно при решении математической задачи понять уравнение означает половину дела. Но формулировка теоремы Ферма очень проста: требуется доказать, что уравнение xⁿ + yⁿ = zⁿ не имеет решения в целых числах при n больше 2. Эндрю не смущало, что самые блестящие умы на Земле потерпели фиаско, пытаясь заново открыть доказательство Ферма. Уайлс немедленно принялся за работу, пытаясь с помощью всей премудрости, которую он только мог извлечь из учебников математики, восстановить утраченное доказательство. А что если ему удастся сделать то, что не удалось никому, кроме Ферма? Обнаружить то, что все проглядели? Уайлс мечтал потрясти мир.

И через тридцать лет Эндрю Уайлсу действительно удалось осуществить задуманное. В аудитории Института сэра Исаака Ньютона он, покрыв всю доску вычислениями и с трудом сдерживая торжество, обернулся лицом к аудитории. Его лекция достигла кульминации, и аудитория сознавала, что наступил великий момент. Один или двое из присутствовавших тайком пронесли на лекцию фотоаппараты, и заключительные замечания Уайлса сопровождались вспышками яркого света.

Держа мел в руке, Уайлс в последний раз повернулся к доске. Последние несколько строк, и доказательство завершено. Впервые за триста лет вызов, брошенный Ферма, получил достойный ответ. Еще несколько камер под блеск вспышек запечатлели исторический момент. Уайлс написал формулировку Великой теоремы Ферма, повернулся к аудитории и сказал: «Думаю, мне следует на этом остановиться».

23 июня 1993 года Уайлс выступил с лекцией в Институте сэра Исаака Ньютона в Кембридже. На снимке вы видите Уайлса через мгновенье после того, как он объявил о найденном им доказательстве Великой теоремы Ферма

Двести математиков вскочили в едином порыве и зааплодировали. Аплодировали все, даже те, кто встретил весть о полученном результате кривой ухмылкой недоверия. Так три десятилетия спустя Уайлс поверил в то, что ему удалось осуществить свою мечту, и после семи лет работы в полной изоляции решился обнародовать итоги своих тайных вычислений. Но пока радость переполняла собравшихся в Институте Ньютона, трагедия уже была готова разразиться. И Уайлс, радуясь вместе со всеми, кто собрался в аудитории, еще не знал о тех злоключениях, которые не замедлили вскоре последовать.