Научные достижения Пифагора и его школы
Научные достижения Пифагора и его школы
Теперь, собственно, настало время для того, чтобы перейти к описанию той сферы деятельности Пифагора, благодаря которой он и стал героем нашей книги. Но прежде, чем перейти к рассказу о научных достижениях пифагорейцев, следует обсудить еще один аспект взаимоотношений Пифагора и его учеников. Речь идет о вопросе, который вызывает у исследователей особый интерес. А именно: присваивал ли Пифагор себе научные достижения своих последователей и приписывали ли пифагорейцы свои открытия учителю. Казалось бы, этот вопрос несложен. Ямвлих пишет:
«У них также был замечательный обычай приписывать все Пифагору и нисколько не присваивать себе славы первооткрывателей, кроме, может быть, нескольких случаев. И действительно, про очень немногих пифагорейцев известно, что они были авторами сочинений».
Долгое время такая точка зрения на данный вопрос была общеизвестной. Но сейчас большинство ученых склоняются к тому, что Ямвлих дает ошибочную информацию. Дело в том, что никто, кроме него, не упоминает о таком обычае. Более того, принято считать, что книга «О пифагоровой жизни», из которой взята данная цитата, не содержит в своей основе каких-либо более древних, а значит — и более достоверных источников. Что же заставило Ямвлиха, жившего через 8 веков после Пифагора, сделать такой вывод? Скорее всего, на подобные мысли его натолкнули распространенные в то время произведения неопифагорейцев, которые приписывались непосредственно основателю учения. Ямвлих прекрасно понимал, что эти сочинения не могут принадлежать Пифагору, и, по всей видимости, сделал вывод о том, что традиция приписывать свои труды учителю бытовала и в раннепифагорейской школе.
При этом следует сказать, что приписываемые Пифагору сочинения начали появляться задолго до Ямвлиха, в III веке до нашей эры. Но эти работы не имели никакого отношения к тем или иным научным проблемам и касались философских, а по большей части — религиозных вопросов. Непосредственной информацией о том, что кто-то из ранних пифагорейцев приписывал свои открытия или работы Пифагору, нет. Поэтому современные исследователи имеют все основания для того, чтобы попытаться выделить из научных достижений пифагорейской школы часть, которая, скорее всего, принадлежала самому Пифагору. Сперва мы отдадим должное математике — науке, с которой имя нашего героя связывает большинство современников.
Долгое время господствовало мнение, что корни древнегреческой математики уходят в исследования древневосточных, египетских, шумерских и вавилонских авторов. Например, египтянам были известны многие теоремы, приписываемые Фалесу и Пифагору, а вавилоняне умели решать квадратные уравнения. Более того, информация о каких-либо математических изысканиях древних греков, производившихся до Фалеса и Пифагора, отсутствует. О восточных корнях своей науки говорили и сами греки.
Такая точка зрения распространена и до сих пор, но единственной не является. Дело в том, что математические знания вавилонян и египтян в основном сводились к решению исключительно утилитарных задач: составление календарей, землемерные работы, строительство, раздел имущества. При этом характер чисто теоретических исследований едва ли был присущ этой математике. Решение же практических вопросов на уровне «у Васи было 4 яблока…» наверняка имело место еще в доисторические времена. Переход к решению математических задач в общем виде, в отрыве от контекста, скорее всего, впервые осуществили и начали широко применять греческие ученые. Они же стали строить систему доказываемых математических положений, впервые применив дедуктивный подход к науке. Поэтому многие современные исследователи считают, что математика как наука зародилась именно в Греции. Также существует довольно серьезный довод в пользу того, что греки не использовали научные данные восточного происхождения. Банальный языковой барьер, который греки крайне редко старались преодолеть, изучая чужие языки, скорее всего, был для них серьезным препятствием. Ярким примером, подтверждающим нежелание греков изучать чужие языки и знакомиться с культурой других народов, являются «Начала» Евклида. Евклид большую часть своей жизни провел в Александрии Египетской. И тем не менее, в самом известном его труде собраны только результаты, полученные или изложенные его соотечественниками. Так или иначе, со времен Фалеса Милетского, предшественника и, возможно, учителя Пифагора, греческая наука развивалась относительно самостоятельно и независимо.
Первым греком, который стал известен своими математическими открытиями, был Фалес Милетский. Его, как и Пифагора, нередко называют родоначальником античной науки. Диоген Лаэртий пишет, что в молодости Фалес совершил поездку в Египет, где обучался астрономии и геометрии у жрецов. Разные авторы приписывают Фалесу доказательство нескольких теорем геометрии:
1 — диаметр делит круг пополам;
2 — в равнобедренном треугольнике углы при основании равны;
3 — вертикальные углы, образованные двумя пересекающимися прямыми, равны;
4 — треугольники равны, если равны два их угла и сторона.
Можно заметить, что эти теоремы вполне могли бы подтверждаться эмпирически, и их справедливость при взгляде на соответствующий чертеж очевидна. Тем не менее Фалес посчитал необходимым доказать их логическим путем. И в результате стал основателем дедуктивного метода в науке. Важно еще и то, что ни египтяне, ни вавилоняне в те времена не имели такого понятия, как величина угла. То есть смело можно считать, что теоремы, приписываемые Фалесу, не были заимствованы у ученых Востока.
Как мы уже писали, биографы называют Фалеса одним из учителей Пифагора. В достоверности этой информации можно сомневаться, но то, что Пифагор был знаком с математическими изысканиями Фалеса, сомнений не вызывает.
Пифагор открыл математические закономерности в музыке. Он обнаружил, что высота звука зависит от длины струны или флейты. Считается, что Пифагор определил отношения этих длин для трех гармонических интервалов. Если длины струн соотносятся как 2/1, то звуки, издаваемые ими, будут отличаться на октаву. Соотношению 3/2 соответствует квинта, 4/3 — кварта. Эксперимент, который помог обнаружить эти закономерности, производился с помощью монохорда. Этот однострунный музыкальный инструмент представлял собой струну, натянутую на линейку, имеющую 12 делений. Пифагор обнаружил, что свободная струна звучит созвучно половине струны (октава). Подобным образом были открыты и два других интервала. Возможно, это открытие основывалось на арифметической теории пропорций, начала которой, следовательно, были заложены ранее и, скорее всего, им же. Или же наоборот, теория пропорций стала непосредственным следствием музыкальных экспериментов. Важность этих опытов состоит не только и даже не столько в обнаружении тех или иных математических закономерностей. Здесь важнее то, что они стали, пожалуй, первыми экспериментами, продемонстрировавшими связь физических законов с законами математики.
Непосредственное указание на то, что именно Пифагор был создателем теории пропорций, есть и в комментариях к «Началам» Евклида Прокла — греческого философа и ученого V века нашей эры. Несмотря на то что Прокла от Пифагора отделяет 10 веков, к его информации можно относиться с большим доверием. Дело в том, что упомянутые комментарии содержат «Каталог геометров», составленный по материалам Евдема Родосского — философа IV века до нашей эры. Вот цитата из этого каталога:
«…Пифагор преобразовал философию геометрии, сделав ее формой образования свободного человека, рассматривая ее начала абстрактным образом и исследуя теоремы с нематериальной, интеллектуальной точки зрения. Он же открыл теорию пропорций и конструкцию космических тел (правильных многогранников, см. ниже)».
Пифагор знал три средние величины:
среднее арифметическое:
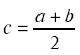
среднее геометрическое:
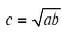
среднее гармоническое:
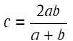
Вполне вероятно, что именно он придумал все эти величины или какие-то из них.
Исследования математических аспектов музыки, по свидетельствам Ямвлиха, привели Пифагора к открытию так называемой «музыкальной» пропорции:
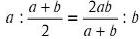
То есть отношение а к среднему арифметическому а и b равно отношению среднего гармонического к b.
В частном виде, при экспериментировании с монохордом можно было получить такое выражение: 12/9 = 8/6. При этом 9 — среднее арифметическое 12 и 6, а 8 — среднее гармоническое. Дальше, скорее всего, были обнаружены и такие равенства: 2/1 = 3/2:3/4. Численно был выражен целый тон, как разница между квинтой и квартой: 3/2:4/3 = 9/8. Естественно, что еще Пифагор и его ученики придали обнаруженным закономерностям, кроме научного, и мистический смысл. Числа, с помощью которых можно было выразить музыкальные интервалы, составили тетрактиду. Вот пример того, как вместе с математической теорией музыки могла развиваться и теория пропорций.
Теперь подробнее рассмотрим теорему, названную в честь нашего героя. Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов двух катетов. И вавилоняне, и египтяне были знакомы с этим утверждением задолго до Пифагора и использовали его знание в практических целях. Конечно же, задаваясь вопросом о том, кто открыл теорему Пифагора, мы, прежде всего, интересуемся тем, кто ее доказал. Споры об этом не прекращаются до сих пор, и вряд ли исследователи когда-нибудь придут к единому мнению по данному вопросу. Сложность решения этой проблемы связана не только с якобы бытовавшей среди пифагорейцев традицией приписывать свои открытия Пифагору. В свидетельствах биографов встречаются противоречия, которые ставят под сомнение авторство Пифагора. Так, Диоген Лаэртий пишет:
В день, когда Пифагор открыл свой чертеж знаменитый,
Славную он за него жертву быками воздвиг.
Долгое время эта цитата считалась серьезным косвенным доказательством того, что на самом деле не Пифагор доказал теорему, названную его именем. Ведь такое свидетельство противоречит представлению о Пифагоре как о вегетарианце и факту, что он учил не приносить в жертву животных. Но, как мы уже писали выше, современные исследователи считают, что запрет на принесение в жертву животных, на самом деле, был приписан ученому позже. Поэтому в качестве серьезного возражения против авторства Пифагора такой довод рассматриваться не может. С другой стороны, есть косвенное подтверждение того, что именно Пифагор первым доказал знаменитую теорему. Дело в том, что ее первое доказательство вполне могло вытекать из той же самой теории пропорций. Предположительно оно могло выглядеть следующим образом.
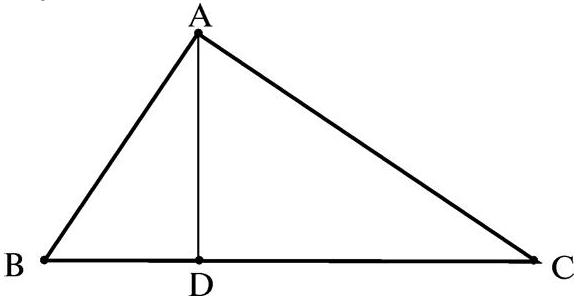
Треугольники ABC, ABD и ACD подобны. Следовательно их стороны пропорциональны:
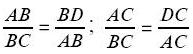
Следовательно:
АВ 2 = BC*BD и АС 2 = BC*DC
Сложив эти уравнения, получаем:
АВ 2 + АС 2 = BC(BD + DC); АВ 2 + АС 2 = ВС 2
Пифагор создал учение о четных и нечетных числах. Он дал определения этим видам чисел и исследовал их свойства. Историки математики считают, что приведенные ниже утверждения из 9-й книги «Начал» Евклида восходят к Пифагору и переданы практически в неизмененном виде.
21. Если складывается сколько угодно четных чисел, то целое будет четным.
22. Если складывается сколько угодно нечетных чисел, количество же их будет четным, то целое будет четным.
23. Если складывается сколько угодно нечетных чисел, количество же их будет нечетным, то и целое будет нечетным.
24. Если от четного числа отнимается четное, то остаток будет четным.
25. Если от четного числа отнимается нечетное, то остаток будет нечетным.
26. Если от нечетного числа отнимается нечетное, то остаток будет четным.
27. Если от нечетного числа отнимается четное, то остаток будет нечетным.
28. Если нечетное число, умножая четное, производит что-то, то возникающее будет четным.
29. Если нечетное число, умножая нечетное число, производит что-то, то возникающее будет нечетным.
30. Если нечетное число измеряет (является делителем) четное число, то оно будет измерять и его половину.
31. Если нечетное число по отношению к некоторому числу будет первым, то оно будет первым и по отношению к его удвоенному.
32. Из чисел, получаемых удвоением от двойки, каждое будет только четно-четным (см. ниже).
33. Если число имеет нечетную половину, то оно будет только четно-нечетным.
34. Если число не будет из получаемых удвоением от двойки и не имеет нечетную половину, то оно будет и четно-четным и четно-нечетным.
Терминология, используемая Евклидом, изложена в начале 7-й книги. Часть из используемых определений, по всей видимости, тоже восходит к Пифагору.
6. Четное число есть делящееся пополам.
7. Нечетное же — не делящееся пополам или отличающееся на единицу от четного числа.
8. Четно-четное число — есть четным числом, измеряемое четным числом (раз).
9. Четно же нечетное есть четным числом, измеряемое нечетное число (раз).
10. Нечетно-четное число есть нечетным числом, измеряемое четное число (раз).
11. Нечетно-нечетное число есть нечетным числом, измеряемое нечетное число (раз).
О том, что именно Пифагор занимался изучением свойств четных и нечетных чисел, свидетельствуют Аристотель и Аристоксен. Едва ли можно предположить, что эти ученые приписывали Пифагору «честь» открытия вполне очевидных истин. Здесь, как и в случае с теоремой Пифагора, заслугой, безусловно, является доказательства приведенных утверждений. Следовательно, ученый впервые применил дедуктивный подход к арифметике.
Единственное незначительное отличие, содержащееся в книге Евклида, состоит в способе доказательства приведенных утверждений. Евклид в данном фрагменте представляет числа в виде отрезков, а Пифагор и его последователи пользовались счетными камешками (псефами). В остальном доказательства, приводимые Евклидом, скорее всего, сходны с доказательствами Пифагора. Интересно, что в восходящем к Пифагору фрагменте «Начал» для некоторых положений даже применяется такой метод, как доказательство от противного. Открытие этого метода также вполне можно приписать Пифагору.
Исследования свойств четных и нечетных чисел стали первыми исследованиями в области теории чисел. Таким образом, нашего героя с полным правом можно назвать основателем этого раздела математики.
Во времена Пифагора и, скорее всего, им самим, также была разработана теория фигурных чисел. Эта теория стала результатом попыток найти взаимосвязь между числами и геометрическими фигурами. Здесь следует несколько подробнее рассмотреть методы счета, используемые пифагорейцами. Для вычислений, как мы уже говорили, они использовали счетные камешки. Их выкладывали на песке, а позже — на счетной доске (абаке) в виде геометрических фигур. Кстати, некоторые источники приписывают изобретение абака Пифагору. Интересно, что при таком взгляде на числа невозможно было представить ноль. Даже единицу считали не числом, а «числовым атомом», а другие числа считали множеством единиц, что и нашло свое отображение в пифагорейской философии.
Рассматривая фигуры, которые образовывали выложенные на песке псефы, Пифагор обнаружил несколько типов фигурных чисел.
Квадратные числа — сумма ряда нечетных чисел, начиная с единицы: 1 + 3 + 5+… + (2n -1) = n2.
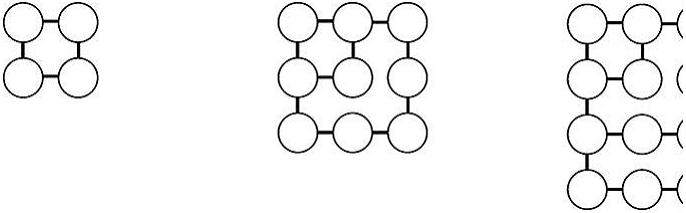
Прямоугольные числа - сумма четных чисел, начиная с 2: 2 + 4 + 6 +...
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКДанный текст является ознакомительным фрагментом.
Читайте также
Приложение 1. Доказательство теоремы Пифагора
Приложение 1. Доказательство теоремы Пифагора Цель доказательства — убедиться в том, что теорема Пифагора верна для всех прямоугольных треугольников. Треугольник, изображенный на рисунке слева, может быть любым прямоугольным треугольником, так как длины его сторон не
«Научные достижения могут быть едиными для всех»
«Научные достижения могут быть едиными для всех» Когда мы говорим о В. И. Вернадском, мы говорим не об истории, а почти всегда о проблемах современности. В чем причина этой удивительной современности В. И. Вернадского?В. И. Вернадский сочетал в себе свойства
Достижения старца
Достижения старца До Тохтамыша еще никогда Тимуру не встречался противник, равный ему силой, и ему стоило немало трудов разгромить Золотую Орду. Тамерланом были даны десять значительных сражений, сто боев, но всякий раз небольшим и маломощным странам, неспособным
Наши достижения
Наши достижения У каждого, конечно, свои странности. У меня их четыре. Я ненавижу:— сидеть в кино,— слушать радио,— ждать поезда,— и давать интервью.От этих вещей меня размаривает сон. И особенно последнее.Но, увы, интервью неизбежны. В особенности перед концертом.Мой
«Достижения есть?»
«Достижения есть?» «Высокий, статный, он постоянно был окружен людьми. Ходил стремительно, большими шагами, и за ним не поспевали. При этом мне всегда вспоминалась картина В. Серова „Петр I на набережной“, — так описывает академик А. П. Виноградов свои впечатления от
УЧЕНИЕ ПИФАГОРА
УЧЕНИЕ ПИФАГОРА Все или почти все религии учат, что душа бессмертна. Греческая религия не составляла исключения. Самое раннее свидетельство тому находим у Гомера. Во время своих странствий Одиссей посетил печальный край киммерийцев, где находится вход в обитель Аида, и
Достижения медицины
Достижения медицины Тем не менее у Кеннеди была одна серьезная слабость, и если бы политические противники о ней узнали, то это положило бы конец его карьере.В 1947 г. после многочисленных безуспешных обследований врачи наконец нашли объяснение целому букету болезней,
Под кровлей Пифагора
Под кровлей Пифагора Как и всегда, после большой операции наступила пауза, необходимая для отдыха и перегруппировки частей. Линия немецкого фронта, отброшенная от Харькова, установилась южнее его, близ железнодорожной линии Люботин — Мерефа, и упирается теперь в речку
Вопрос о происхождении Пифагора
Вопрос о происхождении Пифагора Сведения о происхождении Пифагора достаточно разнообразны и противоречивы. Все источники, однако, сходятся в том, что он родился на острове Самос или происходил из семьи самосца.Диоген Лаэртий передает три версии происхождения Пифагора.
Жизнь Пифагора на Самосе и причины отъезда в Кротон
Жизнь Пифагора на Самосе и причины отъезда в Кротон Если есть достаточные основания полагать, что путешествия Пифагора — лишь плод фантазии его биографов, то отъезд ученого в италийский город Кротон около 531 года до нашей эры — событие вполне реальное. Диоген Лаэртий
Деятельность Пифагора в Великой Греции [15]
Деятельность Пифагора в Великой Греции [15] Кротон был основан как греческая колония в конце VIII века до нашей эры. Греческие колонии в Южной Италии быстро добились процветания (современное слово «сибарит», означающее привыкшего к роскоши праздного и изнеженного человека,
Антипифагорейский заговор и смерть Пифагора
Антипифагорейский заговор и смерть Пифагора Благодаря победе под Сибарисом Кротон стал самым сильным городом Южной Италии и подчинил своему влиянию несколько соседних городов. Политическая сила, которую возглавлял Пифагор, стала очень влиятельной и теперь играла
Религиозные и философские воззрения Пифагора и его последователей
Религиозные и философские воззрения Пифагора и его последователей Конечно же, довольно трудно провести четкую грань между религиозными, философскими и научными взглядами Пифагора и его последователей, ведь пифагорейцы рассматривали все эти аспекты учения как единое
Превратности и достижения
Превратности и достижения В 1947 году 17-летний Джордж уехал из родной страны с суммой денег, которой хватило только на дорогу в один конец. Чтобы как-то существовать, будущему миллионеру приходилось трудиться целыми днями, ведя полуголодное существование. В 1949 году Сорос