Приложение 6. Доказательство гипотезы о трех точках

Приложение 6. Доказательство гипотезы о трех точках

Гипотеза о трех точках утверждает, что невозможно построить точную диаграмму так, чтобы на каждой прямой было по крайней мере три точки. Хотя это доказательство требует минимальных познаний в математике, оно опирается на некоторую геометрическую «гимнастику», и поэтому следует тщательно продумать каждый его шаг.

Начнем с произвольно расположенных точек. Проведем через каждую точку прямые, соединяющие ее со всеми остальными точками. Затем для каждой точки измерим расстояние, отделяющие ее от ближайшей прямой, и найдем ту из точек, которая ближе, чем все остальные, находится от некоторой прямой.

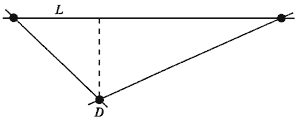
На рисунке внизу изображена такая точка D, которую от прямой L отделяет самое короткое расстояние. На рисунке это расстояние показано штриховой линией. Оно короче, чем расстояние, отделяющее любую другую точку от ближайшей к ней линии. Теперь можно показать, что на прямой L всегда лежат только две точки и что, следовательно, гипотеза верна, т. е. невозможно построить точечную диаграмму так, чтобы на каждой прямой лежали три точки.

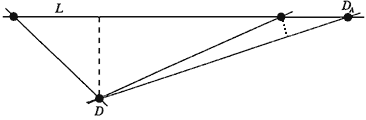
Чтобы показать, что на прямой L должны лежать две точки, рассмотрим, что случилось бы, если бы на ней оказалось третья точка. Если бы третья точка D_A лежала на прямой L вне двух точек, через которые она проходит, то расстояние, показанное пунктирной линией, было бы короче расстояния, показанного штриховой линией. Между тем это расстояние по предположению, наименьшее из всех кратчайших расстояний, отделяющих точку диаграммы от линии. Следовательно, точка D_A существовать не может.

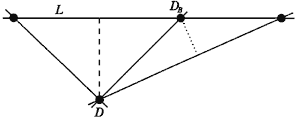
Аналогично, если бы третья точка D_B оказалась на прямой между двумя точками, то расстояние, показанное пунктиром, оказалось бы короче расстояния, показанного штрихом, по предположению наименьшего из кратчайших расстояний от точки диаграммы до прямой.

Следовательно, для каждой конфигурации всегда существует по крайней мере эта прямая, которой принадлежат только две точки диаграммы, и гипотеза верна.