Абсолютное доказательство

Абсолютное доказательство

История Великой теоремы Ферма — это история поиска недостающего доказательства. Математическое доказательство гораздо мощнее и строже, чем представление о доказательстве, которым мы пользуемся в нашем повседневном языке, и даже чем то представление о доказательстве, которого придерживаются физики или химики. Понимание различия между естественнонаучным и математическим доказательствами имеет решающее значение для осознания того, чем занимается каждый математик со времен Пифагора.

Классическое математическое доказательство начинается с серии аксиом — утверждений, которые можно предположить истинными или истинность которых самоочевидна. Затем с помощью логических рассуждений, шаг за шагом, можно прийти к заключению. Если аксиомы истинны, а логика безупречна, то заключение безупречно. Этим заключением и является теорема.

Математические теоремы опираются на такой логический процесс и, доказанные однажды, они остаются истинными до скончания веков. Математические доказательства абсолютны. Чтобы по достоинству оценить значительность абсолютных доказательств, их следует сравнить с их «бедным родственником» — естественнонаучным доказательством, принятым, например, в физике.

В физике гипотеза выдвигается для объяснения какого-нибудь физического явления. Если наблюдения за явлением хорошо согласуются с гипотезой, то это свидетельствует в ее пользу, или, как принято говорить, подкрепляет выдвинутую гипотезу. Кроме того, гипотеза должна не только описывать известные процессы, но и предсказывать исход других процессов.

Для проверки предсказательной силы гипотезы могут проводиться эксперименты, и если они оказываются успешными, то это еще сильнее подкрепляет гипотезу. В конце концов, количество данных, свидетельствующих в пользу гипотезы, может оказаться достаточно большим, и гипотезу принимают в качестве физической теории.

Однако физическая теория никогда не может быть доказана на уровне, столь же абсолютном, как тот, на котором принято доказывать математические теоремы: на основе имеющихся данных физическую теорию можно считать обоснованной лишь с большей или меньшей вероятностью. Так называемое физическое, или, более общо, естественнонаучное доказательство, основано на наблюдениях и данных, доставляемых нашими органами чувств. И те, и другие обманчивы и дают лишь приближение к истине. Как заметил Бертран Рассел: «Хотя это может показаться парадоксом, все точные науки пронизаны идеей приближения».

Даже наиболее широко признанные естественнонаучные «доказательства» неизменно содержат в себе небольшой элемент сомнения. Иногда сомнение становится меньше; но оно никогда не исчезает полностью. Иногда выясняется, что предложенное доказательство неверно. Слабость физического доказательства приводит к научным революциям, во время которых на смену одной теории, считавшейся «верной» приходит другая теория, которая может быть всего лишь уточнением прежней теории, а может полностью противоречить ей.

Например, в поиске фундаментальных частиц материи каждое поколение физиков «перепахивало» или, по крайней мере, уточняло и усовершенствовало теорию своих предшественников. Современный этап поиска мельчайших «кирпичиков», из которых построена Вселенная, начался в первые годы XIX века, когда в результате серии экспериментов Джон Дальтон пришел к гипотезе о том, что все в мире состоит из отдельных атомов и что эти атомы — мельчайшие частицы материи.

В конце XIX века Дж. Дж. Томсон открыл электрон — первую известную субатомную частицу, и атом перестал быть мельчайшей частицей материи.

В начале XX века физики построили «полную» теорию атома: вокруг ядра, состоящего из протонов и нейронов, обращаются электроны. Протоны, нейроны и электроны были горделиво провозглашены физиками полным набором ингредиентов, из которых состоит Вселенная. Затем анализ космических лучей обнаружил существование других элементарных частиц — пионов и мюонов. Еще больший переворот в физике произошел в 1932 году, когда было открыто антивещество — существование антипротонов, антинейтронов, антиэлектронов и т. д. К тому времени физики, занимавшиеся изучением элементарных частиц, не могли с уверенностью сказать, сколько существует различных частиц, но по крайней мере утверждали, что обнаруженные частицы действительно элементарны, т. е. неделимы. Так продолжалось до 60-х годов, когда появилось понятие кварка. Протон, так же, как нейтрон, пион и мюон, оказался состоящим из кварков, несущих электрический заряд, равный дробной части заряда электрона. Мораль всей этой истории в том, что физики непрестанно меняют свою картину мира, а иногда даже стирают ее совсем и начинают рисовать с самого начала. В следующем десятилетии самое представление о частице как о точечном объекте может претерпеть замену на представление о частицах как о струнах — тех самых струнах, которые, возможно, послужат наилучшему объяснению гравитации. Согласно теории струн, трубки длиной в одну миллиардную миллиардной миллиардной миллиардной метра (такие маленькие, что они кажутся точками) могут совершать различные колебания, и каждое такое колебание порождает определенную частицу. Такое представление аналогично открытию Пифагора, обнаружившего, что одна струна лиры может порождать различные ноты в зависимости от того, как она колеблется.

Писатель-фантаст и футуролог Артур Кларк писал, что если какой-нибудь знаменитый профессор утверждает, будто нечто несомненно истинно, то весьма вероятно, что на следующий день это нечто окажется ложным. Физическое доказательство ненадежно и шатко. В то же время математическое доказательство абсолютно и лишено и тени сомненья. Пифагор умер в полной уверенности, что его теорема, бывшая истиной в 500 году до н. э., останется истинной навсегда.

Физика живет, словно подчиняясь решению суда. Теория считается верной, если имеется достаточное количество данных, «неопровержимо» подтверждающих ее предсказания. Иное дело — математика. Она не полагается на данные, полученные в результате могущих оказаться ошибочными экспериментов, а строит свои заключения на основе «железной», т. е. не знающей ошибок, логики. Примером различия между физическим и математическим подходом может служить задача о шахматной доске с выпиленными угловыми полями (рис. 3).

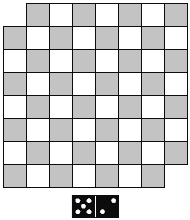
Рис. 3

Перед нами шахматная доска, от которой два противоположных угловых поля отпилили так, что осталось только 62 поля. Возьмем 31 кость домино таких размеров, что каждая кость накрывает ровно два шахматных поля. Вопрос: можно ли разложить 31 кость домино на шахматной доске так, что все 62 поля окажутся покрытыми домино? К решению задачи существуют два подхода.

1) Физический подход

Физик пытается решить задачу экспериментально и, перепробовав с дюжину различных вариантов размещения домино на шахматной доске обнаруживает, что все они заканчиваются неудачей.

В конце концов физик приходит к убеждению, что в его распоряжении достаточно данных, позволяющих утверждать, что покрыть шахматную доску с двумя выпиленными по диагонали угловыми полями невозможно. Однако физик не может быть до конца уверен в том, что это действительно так, потому что может найтись некоторое расположение домино на шахматной доске, которое не было им экспериментально обнаружено, но именно оно и дает решение задачи. Различных же вариантов расположения домино существует не один миллион, и экспериментально проверить всегда можно лишь малую их толику. Что же касается заключения задачи, то это — теория, основанная на эксперименте, и физику не остается ничего другого, как жить под угрозой, что в один «прекрасный» день эта теория может оказаться отвергнутой.

2) Математический подход

Математик стремится решить задачу, выстраивая цепочку логических аргументов, приводящую к заключению, вне всяких сомнений правильному и остающемуся безупречным навсегда. Одна из таких цепочек логических аргументов выглядит следующим образом.

- Оба угловых поля, выпиленные из доски, — белые. Следовательно на доске остались 32 черных поля и только 30 белых поля.

- Каждое домино покрывает два смежных поля, а смежные поля всегда отличаются по цвету, т. е. одно поле черное, а другое — белое.

- Следовательно, независимо от расположения домино на шахматной доске, первые 30 костей, выложенных на доску, должны покрыть 30 белых и 30 черных полей.

- Это означает, что при любом раскладе всегда останется одна домино и два непокрытых черных поля.

- Но любая кость домино покрывает на шахматной доске два смежных поля, а смежные поля всегда отличаются по цвету. Два оставшихся непокрытыми поля одного цвета, и поэтому накрыть их одной костью домино невозможно. Следовательно, покрыть эту доску 31 костью домино невозможно!

Приведенное выше доказательство показывает, что шахматную доску с двумя выпиленными по диагонали угловыми полями невозможно покрыть домино при любом расположении костей. Аналогичным образом, Пифагор создал доказательство, из которого следует, что любой прямоугольный треугольник удовлетворяет его теореме. Для Пифагора понятие математического доказательства было священным, и именно математическое доказательство позволило пифагорейскому братству открыть так много. Большинство современных доказательств невероятно сложны, и разобраться в них неспециалисту просто не по силам. В случае теоремы Пифагора ход рассуждений, к счастью, достаточно прост и опирается только на математику, которую изучают в средней школе. Доказательство теоремы Пифагора изложено в Приложении 1.

Доказательство Пифагора неопровержимо. Оно показывает, что теорема Пифагора выполняется для любого прямоугольного треугольника во Вселенной. Открытие это так потрясло Пифагора, что он в благодарность принес в жертву богам сто быков. [1] Оно стало вехой в развитии математики и одним из самых важных прорывов в истории цивилизации. Значение этого открытия было двояким.

Во-первых, оно позволило сформулировать представление о том, что такое доказательство. Доказанный математический результат обладает более глубокой истинностью, чем любая другая истина, поскольку получен шаг за шагом с помощью логических рассуждений. Хотя философ Фалес Милетский еще до работ Пифагора использовал несколько простых геометрических доказательств, Пифагор развил идею математического доказательства гораздо дальше и сумел доказать более хитроумные математические утверждения.

Во-вторых, теорема Пифагора устанавливает связь между абстрактным математическим методом и чем-то осязаемым. Пифагор показал, что математическая истина приложима к физическому миру и служит его логическим основанием. Математика дает физике строгое начало, а затем, к этому незыблемому основанию физики добавляются наблюдения и измерения, отягощенные ошибками.