Сергей Петрович Дьяков и его вклад в науку

Сергей Петрович Дьяков и его вклад в науку

Г. М. Арутюнян, В. И. Гольданский, Н. М. Кузнецов, А. А. Рухадзе, О. А. Синкевич, Н. Л. Соломина, Л. Г. Степанова

Успехи физических наук. 1993. 163, № 9

В конце 1940-х и начале 1950-х годов на небосводе физической науки ярко вспыхнула звезда, которая недолго горела и внезапно погасла, так и не успев в полном блеске засеять и создать вокруг себя поколения звезд. Это был молодой Сергей Петрович Дьяков, пришедший в науку и очень звонко пропевший свою песню, оказавшуюся лебединой. Лебединой была его песня, поскольку успел он отдать эту песню науке за последние свои 7–8 лет, после чего его жизнь трагически оборвалась: в сентябре 1954 г. он утонул. А годы эти были тяжелые, покрытые густой завесой секретности. Страна залечивала раны после разрушительной войны и в то же самое время спешно, быстрыми темпами создавала ядерный оборонительный щит. Это привело к бурному развитию физической науки, в особенности физики взрыва и гидродинамики. Именно в этой области физики и оставил глубокий след совсем тогда еще молодой Сергей Петрович. Этот след оказался настолько глубоким, что ни завесы секретности, ни беспощадное время не смогли его скрыть и стереть в памяти человеческой. Не случайно, что в вечном учебнике теоретической физики Л. Д. Ландау и Е. М. Лифшица в томе «Механика сплошных сред» [1] весьма скупые на цитирование авторы упоминают имя С. П. Дьякова несколько раз.

Мы, в очень разной степени знавшие Сергея Петровича Дьякова и его работы, решили воспользоваться любезностью главного редактора «УФН» Б. Б. Кадомцева и рассказать о страницах истории физики, написанных Сергеем Петровичем Дьяковым, немного о жизни Сергея Петровича, о том, что он сделал в науке, и о том, как его дело получило дальнейшее развитие. Мы решили сохранить оригинальность восприятия Сергея Петровича и его работ и предоставить слово каждому из нас, без существенной переработки текста воспоминаний. Надеемся, некоторые повторы, в особенности касающиеся личности Сергея Петровича, не будут раздражать читателя.

Первое слово мы предоставили В. И. Гольданскому, нынешнему директору Института химической физики имени Н. Н. Семенова, в котором начал свою научную деятельность С. П. Дьяков в 1946 г. младшим научным сотрудником теоретического отдела, возглавляемого в то время Я. Б. Зельдовичем. В. И. Гольданский — университетский «однокашник» Сергея Петровича и, естественно, раньше всех нас познакомился и оценил его талант как физика.

— При всем старании я не могу восстановить в памяти начало своего официального знакомства с Сережей Дьяковым. Его необычный вид бросился мне в глаза с первой же встречи, видимо, на химфаке МГУ, в 1943–1944 гг., когда я одновременно с работой в лаборатории С. З. Рогинского (тогда она временно находилась не в ИХФ, а в Коллоидо-электрохимическом институте АН СССР — КЭИНе, ныне — Институт физической химии) заканчивал свои студенческие годы в третьем для меня (после Ленинградского и Казанского) университете — Московском.

Пышные черные кудри прогуливавшегося по химфаку юноши, галстукбабочка, сугубо серьезны и вид (почти не помню его улыбающимся) и рассказы о его необычайных способностях — все это заинтриговывало, вызывало любопытство, живой интерес к нему и вместе с тем не всегда доброжелательное отношение окружающих, подозрения в некоем позерстве.

Встречи в университете, где я почти не бывал после окончания, были весьма редкими и ограничивались несколькими малозначащими словами. Поэтому мне было особенно интересно узнать (кажется, в конце 1946 г.) о том, что Сережа поступает на работу в ИХФ, в возглавлявшийся Я. Б. Зельдовичем теоротдел, занятый сверхсекретной деятельностью для И. В. Курчатова и Ю. Б. Харитона (имена которых, впрочем, упоминать не рекомендовалось). Несколько месяцев мы работали в одной комнате, но в совершенно разных амплуа. Я не был посвящен в задачи, которые надо было решать, да и не старался в них вникать, а целые дни сидел у «Мерседеса», играл на его клавишах незнакомую мне музыку, т. е. выполнял чисто техническую работу. Старшими по опыту и значимости вслед за Я. Б. Зельдовичем шли Д. А. Франк-Каменецкий и А. С. Компанеец, но все сулили большое будущее нашим «вундеркиндам» — Коле Дмитриеву и Сереже Дьякову, которые, видимо, уже тогда если и не в полной мере, то достаточно глубоко понимали задачи и сущность расчетов, которыми они занимались, были полноценными творческими членами нашего дружного коллектива «от Якова до Дьякова». То и дело на дверях нашей комнаты появлялся очередной выпуск «двергазеты» со стихами и «трепом», со взаимными дружескими насмешками.

Я. Б. Зельдович и я любили ходить к соседям — в Институт физических проблем на танцы. Появлялся там и Сережа, но ни джазовая музыка, ни резвые прыжки Я. Б. Зельдовича под эту музыку не были ему по душе, и он этого не скрывал. Помню, как один раз Я. Б. даже озлился на это и ехидно спросил: «Что, Сережа, вы, наверно, предпочли бы пляски скоморохов при царе Алексее Михайловиче?» — «Вот именно», — ответил, не уступая шефу, Сергей Петрович. Впрочем, он продолжал посещать вечера в ИФП и добился в танцах заметных успехов.

Частое наше общение длилось, как я сказал выше, всего несколько месяцев. Коля Дмитриев уехал в «Энск» вслед за Я. Б. Зельдовичем (а в двергазете появились стихи А. С. Компанейца «И я пойду, куда велят, чуть сдерживая стон, пойду туда, куда телят гоняет Харитон»), а Сережа Дьяков перешел в ИФП под начало Л. Д. Ландау. Покинул ИХФ и Д. А. Франк-Каменецкий, меня после кандидатской защиты перебросили на эксперименты по нейтронной физике, начались долгие годы нашей близкой дружбы с А. С. Компанейцем, оборвавшейся вместе с его жизнью четверть века спустя. Но гораздо раньше — всего через 5–6 лет — в один из дней ранней осени мы узнали горестную весть о гибели Сережи, утонувшего в одном из подмосковных водохранилищ. В скорбном молчании прощались мы с Сережей в зале ИПФ и проводили на кладбище автобус с его гробом. Несколькими годами спустя я прочел книгу Леопольда Инфельда «Эварист Галуа», и ее эпиграф: «Тот, кого любят боги, умирает молодым. Менандр» — заставил меня вспомнить о Сереже…

После отъезда Я. Б. Зельдовича в город «Энск» теоротдел в ИХФ в течение более чем 20 лет возглавлял А. С. Компанеец, который безгранично был влюблен в Сергея Петровича. И очень жаль, что ему мы не можем предоставить сегодня слово. Но за А. С. Компанейца скажет ученик и продолжатель его дела, заведующий теоретической лабораторией ИХФ Н. М. Кузнецов, которому по роду своей деятельности часто приходилось обращаться к трудам С. П. Дьякова и который так много хорошего слышал о нем от А. С. Компанейца.

— Сергей Петрович — один из тех сравнительно немногих представителей школы Л. Д. Ландау, основные интересы которых были на стыке двух наук — физики взрыва и газовой динамики. Такие ученые имели большой шанс быть вовлеченными в специальные исследования, не подлежащие опубликованию в открытой печати. Сергей Петрович тоже был связан с закрытой тематикой, и его опубликованные работы, о которых мы рассказываем, — лишь часть того, что он успел сделать. И если после нашей статьи найдутся люди, желающие о нем рассказать нечто новое, то статья достигла цели.

Сергей Петрович ушел из жизни очень рано, в начале расцвета творческих сил, успев, однако, оставить яркое фундаментальное научное наследие. Основные опубликованные работы Сергея Петровича, которым исполняется в следующем году 40 лет, посвящены принципиальным вопросам теории структуры и устойчивости ударных волн. Работа Сергея Петровича Дьякова [2] «Об устойчивости ударных волн», безусловно, является классической, не тускнеющей с годами. В ней строгим и изящным методом найдены критерии устойчивости ударной волны относительно искривления ее фронта, определены возможные формы ударной адиабаты, на которой имеются отрезки, удовлетворяющие таким критериям. Эти результаты в последующие годы были подтверждены и уточнены в многочисленных исследованиях, которые ведутся вплоть до настоящего времени (см. обзор [3]). Работа дала искомые ответы и в то же время поставила новые интересные вопросы: наряду с областями устойчивости и неустойчивости была обнаружена загадочная область параметров, в которой начальные малые искривления фронта ударной волны (гофрировочные возмущения) не возрастают, но и не затухают во времени. Каково реальное поведение ударной волны в этой области параметров, устойчива она или нет — ответ на этот вопрос нужно искать, выходя за рамки линейной теории устойчивости. Сергею Петровичу, поставившему эту задачу, не было отпущено судьбой и нескольких месяцев на ее решение. Может быть, поэтому она была решена лишь недавно, спустя более трех десятков лет. Неустойчивость ударной волны согласно критериям С. П. Дьякова соответствует весьма своеобразным формам ударной адиабаты, которые, хотя и не противоречат законам термодинамики, но далеки от типичных. Поэтому результаты С. П. Дьякова воспринимались поначалу главным образом как теоретическое объяснение того, почему ударные волны устойчивы. Однако интерес к проблеме устойчивости ударных волн сильно возрос в 1970-е годы после ряда экспериментальных свидетельств неустойчивости фронта интенсивных ударных волн при ионизации и при некоторых других релаксационных процессах в определенной области параметров. При интерпретации этих явлений классические результаты С. П. Дьякова дали возможность существенно сузить круг неизвестного и отнести наблюдаемые возмущения к проявлению неустойчивости структуры релаксаци онной зоны ударной волны, а не газодинамического разрыва как такового (подробнее см. ниже).

В пионерской работе Сергея Петровича [4] исследована структура ударной волны в двухфазной системе газ+твердые частицы и показано, что концентрация твердых частиц в релаксационной зоне ударной волны меняется не монотонно — проходит через максимум. Этот, казалось бы, чисто академический результат нашел в дальнейшем важное практическое применение в расчетах вероятности воспламенения горючих частиц при ударноволновых воздействиях на запыленные среды. Изучение газовзвесей, особенно с частицами, способными гореть, очень актуально и имеет в наше время все возрастающее прикладное значение в связи с проблемами техники безопасности и охраны окружающей среды. И в этой области науки и техники основополагающие результаты Сергея Петровича служат ориентиром в сложных численных расчетах двухфазных течений конкретных систем. И здесь слово следует предоставить Г. М. Арутюняну, который буквально за несколько месяцев до трагической гибели Сергея Петровича был у него на преддипломной практике и начал работать в этом направлении физики ударных волн.

— О масштабе вклада Сергея Петровича в физику ударныволн в двухфазных средах можно судить по двум примерам из его творческой деятельности, которые приводятся ниже. Значительным вкладом Сергея Петровича Дьякова в гидродинамическую теорию ударных волн является его работа по структуре слабых ударных волн в бинарных газах и взвеси макроскопических частиц (пылинок) в газе, потребовавшая наряду с теплопроводностью и вязкостью, учета также процессов диффузии — термо- и бародиффузии. Эта исключительной сложности задача была корректно сформулирована и аналитически полностью им решена в работе [4]. Здесь с особым блеском проявились его незаурядные физико-математические способности, эрудиция и тонкая интуиция. Наряду с работой [2] она стала основополагающей во всей современной теории устойчивости ударных волн в газах и смесях газов (подробнее см. ниже).

Фундаментальный вклад внес Сергей Петрович в теорию структуры ударных волн в термодинамически неравновесных релаксирующих средах. Известно [1], что вторая вязкость обусловлена нарушением термодинамического равновесия при изменении объема сплошной среды и обычно имеет такой же порядок величины, что и обычная вязкость ?. Однако если время релаксации не мало по сравнению с характерным временем изменения объема, то отклонения от термодинамического равновесия велики и диссипация энергии может быть большой. Поскольку диссипация определяется второй вязкостью ?, значение ? может оказаться большим. Величина ? зависит от соотношения между скоростью изменения объема и временем релаксации. В частности, если изменения объема вызваны звуковой волной, то ? зависит от ее частоты и можно говорить о дисперсии второй вязкости. М. И. Мандельштам и М. А. Леонтович, исследовавшие этот вопрос еще в 1937 г., показали, что [5]

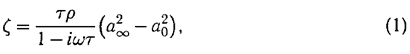
где ? — плотность среды, ? — частота, i — мнимая единица, a_?, a₀ — скорости звука при частотах столь больших и малых, что релаксационный процесс соответственно «заморожен» и, наоборот, полностью завершился. Из (1) следует, что при процессах настолько медленных, что ?? << 1,

откуда следует, что ? действительно растет с увеличением времени релаксации ?.

С. П. Дьяков в 1954 г. показал [6], что формула (2) и условие ее выполнения могут быть эффективно использованы для определения структуры и ширины слабых ударных волн в сильно релаксирующих средах. Действительно, в соответствии с гидродинамической теорией ударных волн [1] давление в переходном слое слабой ударной волны (т. е. ее структура) определяется в соответствии с законом

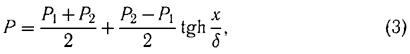
где x — пространственная координата, P₁, P₂ — давление соответственно впереди и за фронтом волны, а ? — ее ширина, определяемая формулой

где V, S — удельные объем и энтропия, ?P = P₁ — P₂ — перепад давления в ударной волне, а

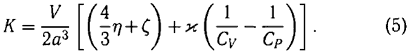
В формуле (5) a, C_V , C_P — скорость звука и удельные теплоемкости при постоянных давлении и объеме, а все входящие а правую часть (4) величины (кроме ?P) относятся к состоянию перед волной. С. П. Дьяковым было замечено, что поскольку в силу (4) ширина переходного слоя ударной волны обратно пропорциональна ее амплитуде, то для достаточно слабых ударных волн в редактирующей среде состояние вещества в переходном слое можно считать изменяющимся медленно по отношению к установлению равновесия, что позволяет трактовать процесс релаксации в духе метода Мандельштама-Леонтовича с использованием выражения (2) в (5), пренебрегая при этом теплопроводностью и обычной вязкостью. В результате была получена формула

возможность пользования которой требовала установления еще условия медленного изменения состояния вещества в переходном слое. Сформулированное в общем виде ? >> a₀?, в силу (2) и (6) это условие было конкретизировано в форме общеизвестного ныне критерия

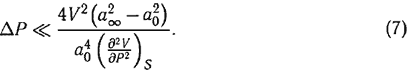
Описанный выше метод нашел приложение для некоторых важных классов релаксирующих систем [7–9] и в настоящее время широко известен как «метод концепции второй вязкости Мандельштама-Леонтовича-Дьякова».

Как уже отмечалось выше, проблема устойчивости фронта ударной волны вновь стала в центре внимания исследователей с начала 1970 г., когда это явление получило подтверждение экспериментом, а работа Сергея Петровича [2] — дальнейшее развитие. Ряд обобщений и идей в этой области принадлежит О. А. Синкевичу, которому мы и предоставим слово.

— В настоящее время становится очевидным, что именно механизм устойчивости обеспечивает отбор различных эволюционирующих состояний в живой и неживой природе. Если останавливаться только на неустойчивостях в распределенных системах, то во многих случаях можно выделить неустойчивости, вызванные внутренними состояниями и процессами в среде, и неустойчивости, обусловленные активными границами.

С. П. Дьяков был одним из первых, кто убедительно продемонстрировал роль активных границ в задаче об устойчивости плоских ударных волн с произвольным видом ударной адиабаты Гюгонио P = P(V)_H (здесь P — давление, V = 1/? — удельный объем, а ? — соответственно плотность среды) относительно двумерных гофрировочных возмущений. Для плоской ударной волны, распространяющейся в положительном направлении оси y, когда невозмущенная плоская поверхность фронта совпадает с плоскостью x0y, Сергей Петрович исследовал в линейном приближении устойчивость первоначально малых возмущений ? (вязкостью и теплопроводностью пренебрегалось) вида ? ~ exp(ikx — i?t). Поскольку ударная волна движется со сверхзвуковой скоростью относительно газа перед фронтом волны, то, естественно, возмущения туда не проникают. Для линеаризованных уравнений газодинамики выбирались следующие граничные условия: ограниченность возмущений при z ? ? и соотношения на фронте ударной волны, вытекающие из обычных законов сохранения потоков массы, импульса и энергии. Полагая произвольной форму ударной адиабаты, выделяя возмущения в энтропийновихревой и звуковой волнах, С. П. Дьяков из решения характеристического уравнения получил условия неустойчивости плоской ударной волны относительно гофрировочных возмущений в виде

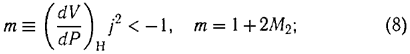
здесь j = ?₁v₁ = ?₂v₂ — поток массы через фронт ударной волны, M₂ = V₂/a_S2 — число Маха, v₂ — скорость среды за фронтом, a_S2 — скорость звука за фронтом ударной волны, (dV/dP)_H — производная от ударной адиабаты, индексы 1 и 2 относятся соответственно к состояниям перед фронтом и за фронтом ударной волны.

Кроме условий (8) неустойчивости ударной волны С. П. Дьяков установил, что в области параметров, удовлетворяющих условию

где

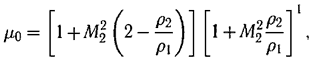
существуют решения с незатухающими возмущениями фронта волны (стационарными в некоторой системе координат, скользящей вдоль фронта), к которому со стороны зафронтового течения примыкают звуковые волны, исходящие под определенным углом. Область параметров

была отнесена С. П. Дьяковым к области устойчивости плоских ударных волн относительно малых гофрировочных возмущений.

Последующие многочисленные исследования устойчивости плоских ударных волн [10–11], выполненные различными методами, не изменили границ области возникновения неустойчивости (8). Учет вязкости и теплопроводности газа [14, 15] также не изменили положение границ области (8). Однако уточнения нижней границы области (9), проведенные в работах {9-12, 16], показали, что

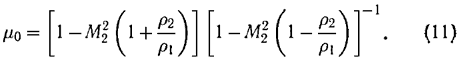
Дальнейший, более детальный анализ характера проведения малых возмущений показал, что в устойчивой области, если не учитывать вязкость и теплопроводность газа, возмущения ударной волны могут затухать во времени по степенному закону t^-3/2 (возмущения в сильной ударной волне затухают по закону t^-1/2). Учет конечной вязкости [13] или конечной проводимости среды за фронтом ударной волны, движущейся в поперечном магнитном поле, может приводить к экспоненциальному затуханию возмущений и к исчезновению области спонтанной генерации звука [19, 20].

В области (9) существования незатухающих (стационарных) гофрировочных возмущений фронта углам ориентации исходящих звуковых волн соответствует резонансное отражение звука фронтом ударной волны [22–25]. В этой области параметров задачи ударная волна, будучи нейтрально устойчивой к малым возмущениям, может оказаться неустойчивой к возмущениям конечной амплитуды, приводящим к расщеплению ударной волны на ударную волну меньшей интенсивности, контактный разрыв и длину разрежения [26–35]. Неустойчивость плоской ударной волны относительно одномерных возмущений тесно связана с эволюционностью поверхности разрыва — фронта ударной волны [22]. В дальнейшем было исследовано поведение малых возмущений на нелинейной стадии для неустойчивой ударной волны [25–35], когда на фронт волны подает конечное возмущение [27] и самопроизвольный распад [31, 32], приводящий для двумерных возмущений распад плоской волны на тройную конфигурацию — скачок [31]. Однако полного ответа на вопрос о характере явлений в неустойчивой области в настоящее время еще нет.

Проблема неустойчивости плоской ударной волны относительно двумерных возмущений тесно связана с тем, что двумерные возмущения могут обладать бесконечно большим коэффициентом роста

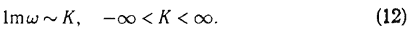
Учет конечной толщины фронта ударной волны — структуры волны, связанной с конечной вязкостью и (или) теплопроводностью, процессами химической кинетики, процессами ионизации, — может приводить к ограничению инкремента роста возмущений и нахождению возмущения, выживающего на нелинейной стадии. Можно предположить, что эволюция неустойчивой ударной волны и конечная стадия, в которую переходит неустойчивое состояние, тесно связаны с видом начальных возмущений — в зависимости от вида возмущений ударная волна может переходить в различные состояния.

Любопытная ситуация может существовать в области нейтральных колебаний даже в отсутствие химических реакций в зоне за фронтом волны, если рассматривать ее структуру. Нейтральноустойчивая ударная волна может генерировать турбулентность (при этом естественным образом возникает непрерывный спектр возмущений). Возникновение турбулентности может приводить не только к модификации коэффициентов переноса турбулентной вязкости и теплопроводности, но и изменять вид гидродинамических уравнений, описывающих поведение газа за фронтом волны: система осредненных уравнений Навье-Стокса, замыкающие уравнения для интенсивности турбулентных пульсаций. Поскольку в области нейтральных колебаний ударная волна неустойчива к возмущениям конечной амплитуды, возникновение турбулентных пульсаций выделяет интенсивность возмущений (порог), которые могут приводить к распаду волны на другие устойчивые конфигурации. Еще больший набор возможностей возникает для ударных волн в двухфазных средах и многокомпонентных плазмах, и здесь подходы, предложенные С. П. Дьяковым, могут оказаться весьма продуктивными.

— Но не только физиком-теоретиком от Бога был С. П. Дьяков. От Бога был его талант лектора. Ему не было 28 лет, когда он читал нам (Г. М. Арутюняну и А. А. Рухадзе), студентам 4-го и 5-го курсов физикотехнического факультета МГУ и факультета теоретической и экспериментальной физики МИФИ, спецкурс по нестационарным и нелинейным явлениям в гидродинамике. Во многом соответствующие главы «Механики сплошных сред» Л. Д. Ландау и Е. М. Лифшица напоминают содержание лекций С. П. Дьякова. А ведь книга эта тогда, когда он читал свои лекции в 1952 и 1953 гг., еще не была издана. А после издания всем, кто слушал спецкурс С. П. Дьякова, стало ясно, почему так часто его фамилия упоминается в этой книге. Книга Л. Д. Ландау и Е. М. Лифшица «Механика сплошных сред» вышла уже после гибели С. П. Дьякова.

А как он читал этот курс! Надо было видеть этого очень худого молодого человека у доски! С большой черной шевелюрой, в коричневом полосатом костюме, он был похож на Ван Клиберна, но только брюнета, на восторженного дирижера в манере держаться и обращаться с доской, как с оркестром, и с мелом, как с дирижерской палочкой. Влюблен он был в науку, как Жюльен Сорель, и она отвечала взаимностью. Не случайно он так много успел сделать в науке и оставил столько воспоминаний о себе. По его влюбленности во все, о чем он рассказывал, по восторгу было видно, что он не пересказывает учебники или даже статьи, только что опубликованные другими авторами, а излагает свое, полученное им и потому так дорогое ему. Во всем чувствовалось, что это только что, вчера полученный результат. И Сергей Петрович не боялся рассказывать о своих еще не опубликованных результатах. Не боялся потому, что он знал все это, только что им полученное, столь глубоко, что вряд ли кто, кроме Л. Д. Ландау мог бы подхватить его идею и обогнать его. Но и ему С. П. Дьяков не боялся рассказывать о своих мыслях и сомнениях, так как был влюблен в него и об этом часто на лекциях признавался так: «Все, что я вам рассказываю, подсказал мне Л. Д. Ландау, это родилось в беседах с ним».

И был счастлив С. П. Дьяков, что пользовался ответным уважением Л. Д. Ландау. Он этим не хвастал, это следовало из произнесения им имени Л. Д. Ландау, которое всегда произносилось с придыханием. А взаимность этого восхищения видна из книги Л. Д. Ландау и Е. М. Лифшица.

По мере того как мы вслушивались в лекции Сергея Петровича и втягивались в его семинарские занятия, мы понемногу начинали понимать, что он открывает перед нами двери в уникально интересный и необычный мир процессов, где сложнейшие физические явления стремительно и колдовски, замысловатым образом развиваются в пространстве и во времени. Становилось очевидным, что предмет, которым нам предстояло заниматься, по своей нетривиальности, проблемности и внутренней красоте ничуть не уступает объектам, изучаемым в электродинамике, квантовой механике или ядерной физике.

Именно лекции Сергея Петровича Дьякова убедили нас в правоте услышанных нами значительно позже слов великого Гейзенберга, что «механику сплошных сред он считает самым интересным разделом теоретической физики». Эти слова мог произнести каждый, кто тогда слушал лекции С. П. Дьякова.

Говорить и писать о С. П. Дьякове одновременно и легко и трудно. Легко потому, что он был натурой откровенно яркой и незаурядной. А трудно, поскольку он был непрост и определенно замкнут. В отношениях со студентами он был достаточно открыт, терпим и демократичен. На лекциях и семинарах давал расслабляться, блистая часто остроумием. Все, например, помнят его шутку о трех необходимых качествах теоретика (холодная голова, горячее сердце и свинцовый зад), когда на одном из семинаров никто из троих, подошедших к доске, так и не решил какую-то задачу. Однако он знал меру и никогда не переходил ту грань, за которой его отношения со студентами могли потерять взаимоуважительность.

Незаурядность и изысканность Сергея Петровича проявлялись буквально во всем. Даже во внешнем его облике. Одевался он со вкусом, но без излишеств. Всегда аккуратный, по тем временам несколько старомодный (носил длинные волосы и бабочку). Юмор его тоже был нестандартным. Известно, что С. П. был заядлым туристом. И когда однажды он рассказывал о своем походе по пескам Кара-Кумов и его спросили, не слишком ли жарко там было, он экспромтом ответил: «А вы как думаете, если ночью температура опускалась до плюс сорока по Цельсию?»

О скромности Сергея Петровича. Когда он читал свой курс, а ему, как выяснилось, тогда еще не было даже 28 лет, никто из нас и не подозревал, что он уже был лауреатом Государственной премии за работы совместно с выдающимися физиками Я. Б. Зельдовичем и А. Д. Сахаровым. А знают ли об этом сегодня даже те, кто знал его тогда?

Во всем облике, таланте и трагической судьбе С. П. Дьякова было что-то моцартовское, в том числе и ранний расцвет его таланта. Об этом свидетельствует вся его биография, о которой рассказывали друзья Сергея Петровича — Н. Л. Соломина и Л. Г. Степанова.

— С. П. Дьяков родился 29 августа 1925 г. в Москве, в семьеинженера-мостостроителя. Дедом его был ученый-лесовод Сергей Васильевич Дьяков, упомянутый в энциклопедии Брокгауза и Эфрона. Дома его родители создавали атмосферу высоких духовных интересов, которая и сформировала впечатлительную натуру Сергея Петровича.

В 14 лет Сережа в своем классе в школе вел уроки химии, когда заболевал учитель. В 15 лет Сережа добился разрешения Наркомпроса на сдачу экзаменов в МГУ экстерном и в 16 лет, когда началась война, стал студентом химфака МГУ. Одновременно с химфаком он факультативно закончил мехмат университета и, по отзывам профессуры факультета, обладал блестящими математическими способностями.

В 17 лет Сережа стал сиротой — умер от туберкулеза его отец, и он стал кормильцем семьи — матери и брата. А в 22 года потерял и брата. Средства к жизни Сережа добывал частными уроками по математике. Будучи студентом и аспирантом, он очень нуждался.

Учась на химфаке, Сережа посещал семинары по теоретической физике профессоров Д. Д. Иваненко и Н. Н. Боголюбова. В 1944 г. Сережа прочел доклад «Статистический метод Гиббса», обнаружив при этом великолепные ораторские способности; позже с успехом прочитал доклад в большой физической аудитории физфака МГУ «О законе сохранения энергии», собрав полную аудиторию. В эти годы Сережа увлекался квантовой механикой, работами Шрёдингера, Гейзенберга, Планка и других.

В 20 лет Сережа досрочно окончил химфак и поступил в аспирантуру физического факультета по кафедре теоретической физики.

В 23 года С. П. Дьяков защитил кандидатскую диссертацию, работая уже в Институте химической физики Академии наук. Он выполнил ряд работ, к сожалению, не полностью освещенных в печати, по гидродинамике взрыва и ударным волнам в сплошных средах. В 1951–1954 гг. он работал с Л. Д. Ландау в Институте физических проблем АН СССР, был его сподвижником в гидродинамике и стал в этой области в один ряд с ним.

Л. Д. Ландау и Е. М. Лифшиц во многом опирались на научные труды Сергея Петровича при создания раздела «Механика сплошных сред» знаменитого курса теоретической физики.

В 1953 г. Сергей Петрович был удостоен Государственной (тогда Сталинской) премии совместно с Я. Ю. Зельдовичем за участие в разработке и реализации проекта атомной бомбы и ордена «Знак почета».

Сергей Петрович был музыкально одаренным человеком, играл на фортепьяно и скрипке, пел и даже хотел поступать в училище имени Гнесиных по классу вокала, куда его настойчиво приглашали. Он глубоко понимал музыкальную классику, очень любил Вагнера, Чайковского, Скрябина, Шумана, Шуберта. Обладал романтической внешностью: высокий, стройный, с одухотворенным прекрасным лицом, живыми насмешливыми глазами. Ранимость своей души он прикрывал иронией, игрой ума. Артистичность его натуры проявлялась и в черном бантике, который он неизменно надевал.

В его лице наука потеряла талантливого ученого с ярким интеллектом, богато одаренного человека, благородную душу. Разумеется, он сделал бы еще очень много и многие были бы осчастливлены его талантом и добротой. Но нам кажется, что и то, что он сделал, хорошо известно далеко не всем. И мы надеемся, что эта статья найдет отклик в сердцах многих, кто его знал и знал его деятельность, особенно в закрытой в те годы области физики.

Литература

1. Ландау Л. Д., Лифшиц Е. М. Механика сплошных сред. М.: Гостехиздат, 1953.

2. Дьяков С. П. // ЖЭТФ. 1954. 27, № 3. С. 288.

3. Кузнецов Н. М. // УФН. 1989. 159, № 3. С. 493.

4. Дьяков С. П. Ударные волны в бинарных смесях // ЖЭТФ. 1954. 27, № 3. С. 283–287.

5. Мандельштам Л. И., Леонтович М. А. К теории поглощения звука в жидкостях // ЖЭТФ. 1937. 7, № 3. С. 438–449.

6. Дьяков С. П. Ударные волны в релаксирующей среде // ЖЭТФ 1954. 27, № 6. С. 728–734.

7. Арутюнян Г. М. Слабые ударные волны в терморелаксирующей среде // Докл. АН СССР. 1969. 185, № 4. С. 778–781.

8. Арутюнян Г. М. О структуре слабых ударных волн в релаксирующих средах // Прикл. мех. и теор. физика. 1969. 2. С. 110–115.

9. Арутюнян Г. М., Овсепян С. Т. Структура слабых ударных волн при фазовых переходах первого рода // Изв. АН СССР. Мех. жидкости и газа. 1980. № 4. С. 55–62.

10. Конторович Б. М. // ЖЭТФ. 1957. 33, № 6(12). С. 1525.

11. Иорданский С. В. // Прикл. матем., мех. 1957. 21. № 4. С. 465.

12. Freeman N. S. // Proc. Roy. Soc. A. 1955. 228. P. 1174.

13. Whitman G. B. // J. Fluid. Mech. 1957. 2. P. 145.

14. Зайдель Р. М. // Прикл. матем., мех. 1960. 24, № 4. С. 30.

15. Morduchow M., Paullay A. J. // Phys. Fluids. 1971. 14, N 2. Р. 323.

16. Асланов С. К. // Дифф. уравнения. 1966. 2, № 8. С. 1115.

17. Плешанов А. С. // Физ. горения и взрыва. 1968. 4, № 1. С. 95.

18. Николаев Ю. М. // Прикл. матем., мех. 1965. 29, № 2. С. 658.

19. Синкевич О. А. // Теплофиз. высоких температур. 1969. 7, № 6 С. 1126.

20. Синкевич О. А. // Изв. АН СССР. Мех. жидкости и газа. 1972. № 11. С. 122.

21. Барышников А. С., Скворцов Г. Е. // Журн. технич. физики. 1979. 49, № 11. С. 2483.

22. Ландау Л. Д., Лифшиц Е. М. // Гидродинамика. М.: Наука, 1986.

23. Дьяков С. М. // ЖЭТФ. 1957. 33. С. 962.

24. Конторович В. М. // Акуст. журн. 1959. 5. С. 314.

25. Кузнецов Н. М. // ЖЭТФ. 1986. 90, № 2. С. 744,

26. Кузнецов Н. М. // Докл. АН СССР. 1984. 277, № 1. С. 65.

27. Gordner C. S. // Phys. Fluids. 1963. 6. P. 1366.

28. Swan C. W, Fowles J. P. // Ibid. 1973. 18. P. 28.

29. Fowles J. P. // Ibid. 1976. 19. P. 227.

30. Егорушкин С. А. 11 Изв. АН СССР. Мех. жидкости и газа. 1982. 6. С. 147.

31. Егорушкин С. А. // Там же. 1984. 3. С. 1107.

32. Кузнецов Н. М. // ЖЭТФ. 1985. 88, № 2. С. 470.

33. Fowles J. P., Howing A. F. // Phys. Fluids. 1984. 27. P. 1981.

34. Magda A., Rosales R. // Ann. Math. 1984. 71. P. 117.

35. Erpenbek J. J. // Phys. Fluids. 1982. 5. P. 1181.

36. Мишин Г. И., Бедин А. П., Юшенкова Н. И. и др. // Журн. технич. физики. 1981. 51. С. 2315.