2.0.0. Отношения элементов друг к другу

2.0.0. Отношения элементов друг к другу

2.1.0. Исследуя отношения элементов друг к другу, мы вступаем в сферу бесконечного множества конечных состояний: это область разнообразнейших событий, неисчерпаемого богатства вещей и явлений, но это также область того, что не имеет основания в самом себе, не принадлежит себе, а принадлежит другому — целостности Мира, той уникальной системе, интегральные свойства которой не могут быть сведены к свойствам ее составляющих. Эта особенность элементов — принадлежать другому, находит здесь свое проявление в том, что их множественность и взаимное противостояние имеют своим основанием общие границы, а бесконечная смена событий — инвариантность и постоянство закона, по которому эти изменения совершаются.

Любой элемент или, скажем проще, любой предмет окружающей нас среды, представляется обыденному сознанию чем-то вроде кошелька или узелка, в котором связаны вместе все свойства этого предмета.

Достаточно запустить в этот узелок руку, чтобы вытащить то, что там заранее приготовлено.

Увы, такое простое и удобное представление ошибочно. В действительности дело обстоит иначе. Раскройте любой учебник физики. Каждое определение, с которым вы столкнетесь, предстанет перед вами как отношение. Попробуйте размотать клубок этих отношений до конца, чтобы найти первоначало всех вещей и явлений. Это вам не удастся. Самые фундаментальные понятия — это снова и снова отношения, образующие зачастую порочный круг или оперирующие с неизвестными. Релятивистская масса вещества, например, определяется через отношение полной энергии к квадрату скорости света m = E/c 2: одно неизвестное (масса) определяется отношением другого неизвестного (энергия) к константе (к квадрату скорости света). Но «…физике сегодняшнего дня, — писал Р. Фейнман, — неизвестно, что такое энергия» [9, т. 1, с. 7]. Однако знания отношений оказывается достаточно, чтобы решать самые сложные задачи, в том числе и сугубо практические. Итак, отношение элементов друг к другу — это первое и основное, что мы здесь отмечаем. Вне каких-либо отношений охарактеризовать предмет, частицу, элемент вообще невозможно.

Второе: все свойства элементов в сфере межэлементных отношений обнаруживаются при их взаимодействии, точнее, при их близкодействии, т. е. тогда, когда между ними возникает граница. Но границы не являются собственностью ни одного из противостоящих друг другу элементов — это их общий предел, общее достояние. Следовательно, как первое, так и второе наблюдение указывает нам одно направление, следуя которому мы только и можем надеяться найти основание всех вещей и явлений.

Это основание есть, по нашему мнению, сама система, к которой принадлежит элемент, а, в конечном счете, это — Мир в целом.

Таким основанием не может быть никакая элементарная или сверхэлементарная частица, потому что она, чтобы быть чем-то, должна отличаться от других частиц или вообще от всего того, что не является таким элементарным началом.

А если так, то она должна обладать своей собственной сущностью, которая и была бы таким основанием, но сущность, как мы видели (см. дополнение к тезису 1.4.0), есть не что иное, как интегральное свойство системы, т. е. свойства такой реальности, которая не является элементарным началом. Если же нечто не обладает сущностью, то оно лишено внутреннего единства, не тождественно самому себе (x??x) т. е. является пустым множеством — оно уже не нечто, а ничто.

Против существования элементарного первоначала может быть высказано еще и такое соображение. Если бы оно действительно существовало, оно было бы такой частицей, которая находится в начале всей иерархии систем, но сама не является системой. Однако по мере того как мы ведем поиск путем разъятия систем на элементы, мы утрачиваем одно за другим интегральные свойства систем и этот процесс должен быть продолжен до тех пор, пока не будут исчерпаны все системы, а когда это произойдет и мы, наконец, будем как будто у цели, то окажется, что самой частицы вообще нет и именно потому, что она только частица, а не система, и, следовательно, лишена всех системных или, иначе говоря, всех интегральных свойств, а вместе с этим и собственной сущности.

2.2.0. Действительно, порождаемые внутрисистемными отношениями границы противостоящих друг другу и взаимодействующих элементов, не становятся для них третьим промежуточным объектом, а принадлежат сторонам совместно, являясь их общим пределом. Математика определяет границу как «множество точек подпространства A данного топологического пространства x, обладающих тем свойством, что любая окрестность каждой из них содержит как точки из A, так и точки из xA» [6, т. 1, с. 1095]. Очевидно, что утверждение, высказанное в тезисе 2.2.0, не противоречит приведенному здесь определению границы. Только здесь математика ведет речь о пространственной границе, я же говорю о границе вообще. Однако и тут и там отмечается одна, с моей точки зрения, важная особенность границы, на которую часто не обращают достаточного внимания. Эта особенность сформулирована в тезисе 2.3.0.

2.3.0. Будучи общим пределом элементов, границы не только разделяют их друг от друга, внося в них определенность, но в той же степени и объединяют их между собой. Именно здесь, на межэлементных границах, актуализируется бесконечное множество конечных свойств элементов, которые, строго говоря, не принадлежат ни одному из них, взятому отдельно, вне системы, а являются результатом их взаимного соотнесения.

Итак, граница снижает степень неопределенности пограничных элементов, а, следовательно, повышает количество информации о них. Например, границей трехмерного тела будет двумерная поверхность; границей поверхности будет линия, границей линии — точка. Вероятно, точка может рассматриваться как граница пространства и времени. Если точку обозначить как a0 (при a? 0)), одномерное пространство как a1, двумерное как a2, и трехмерное как a3, тогда степень их неопределенности H, выраженная в битах, будет: для точки H1 = — log2 a0; для одномерного пространства H2 = — log2 a1; для двумерного — H3 = — log2 a2. Эта закономерность может быть обобщена и на границу n-мерного пространства, степень неопределенности которого будет: Hn+1 = — log2 an. Все это подтверждает сказанное о том, что граница снижает степень неопределенности элемента или, что то же самое, — увеличивает количество информации о нем.

Что же касается мысли о том, что свойства элементов, которые актуализируются на их общих границах, не принадлежат единолично ни одному из них взятому отдельно, вне системы, то она, эта мысль в поэтической форме была высказана в древней Индии. Я имею в виду жемчужную сеть Индры, которая «…отражается в каждой жемчужине, а жемчужина, в свою очередь, вместе со всей отраженной сетью отражается в другой жемчужине». [12, с. 126].

2.4.0. Но граница, как предел, — не состояние, а процесс — внутренне движение элементов к взаимопроникновению, к единству. На этом пути возникает бесконечное множество различных композиций, обладающих разной степенью устойчивости или инвариантного повторения. Инварианты, которые пронизывают собой межэлементные отношения и цементируют их структуры, опираются на внутренние законы системы, которые обладают иерархическим строением. К числу наиболее фундаментальных инвариантов принадлежат различные виды симметрии и пространственно-временная упорядоченность элементов. Причем, место, занимаемое той или иной композицией межэлементных отношений на иерархической лестнице инвариантов, а, следовательно, и ее значение, определяется степенью их универсальности. Из двух названных выше инвариантов — симметрии и пространственно-временной упорядоченности, — большей универсальностью обладает симметрия, ибо межэлементные отношения, которые упорядочены в пространственно-временные композиции, обязательно содержат в себе симметричные элементы, а симметричные элементы могут и не быть упорядочены в пространственно-временные конструкции.

Математическая модель, освобождающая изучаемый нами объект или процесс от второстепенных, для данного случая, характеристик, значительно упрощает решение многих задач, которые ставит перед нами наша деятельность. Воспользуемся этим, чтобы установить здесь первородство некоторых фундаментальных признаков.

Прежде всего, вспомним о существовании следующих математических операций:

Таблица 2.4.1.

Знаком обозначен один внутренний закон множества, например, сложение; знаком обозначен другой внутренний закон множества, например, умножение.

Далее, прослеживая использование этих операций в формировании алгебраических структур, расположим эти структуры в том порядке, который поможет нам установить степень их инвариантности, а стало быть, и универсальности.

Таблица 2.4.2.

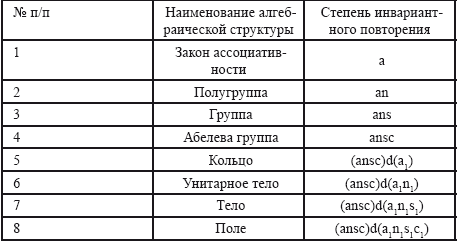
Оказывается, что наибольшей инвариантностью обладает закон ассоциативности (a), который пронизывает все названные структуры, а также те композиции, которые здесь не названы, но могут быть получены из упомянутых путем их дальнейшего усложнения. К таким усложненным композициям относятся, например, пространства.

Чтобы не быть голословным и показать их сложную структуру, приведу определение одного из них, а именно векторного пространства:

«Пусть даны: 1) тело K, элементы a, b… которого будут называться коэффициентами или скалярами; 2) модуль (т. е. аддитивная абелева группа) M, элементы x, y… которого будут называться векторами; 3) умножение x a векторов на скаляры, удовлетворяет следующим требованиям:

B1. x a лежит в M

B2. (x + y) a = x a + y a

B3. x (a + b) = x a + x b

B4. x (a b) = (x a) b

B5. x 1 = x

Если все это выполнено, то M называется векторным пространством над K…» [4, c. 82].

А если математическим абстракциям в действительном мире что-то соответствует, и математические модели, которые нашли столь широкое практическое применение в различных областях знания, моделируют реальные процессы, то, основываясь на приведенной выше иерархии инвариантов, можно утверждать, что есть обширная и вполне реальная область межэлементных отношений, которая существует вне или до пространства, потому что пространство представляет собой более сложную по сравнению с ними композицию. К таким элементарным допространственным отношениям и принадлежат все перечисленные в таблице 2.4.2 структуры.

Но тут мне могут возразить так: позвольте, вы утверждали раньше, что основанием элементов не могут быть элементарные частицы, а что ими являются системы. Теперь вы ведете речь об инвариантах и ищете атомарные отношения, которые инвариантны всему и все собой пронизывают. Не является ли это утверждением того, что раньше, правда, в другой форме отрицалось? Отвечаю: думаю, что нет, и вот почему: к универсальной элементарной частице сводилось все, предполагалось, что из нее состоит весь разнообразный мир, все частицы, все элементы; иерархия же инвариантов содержит различные отношения: каждый тип отношений не сводим к другому, они добавляются друг к другу, как бы нанизываются на воображаемый стержень.

Каждое из этих отношений порождено системой, ее интегральными законами, которые и обусловливают собой ту или иную структуру целостности.

Инварианты и вся их иерархия цементируют систему элементов, реализуют ее единство.

Теперь об универсальности приведенных выше структур. Она следует по убывающей в том порядке, в котором структуры расположены в таблице 2.4.2. Отсюда, в частности, следует, что симметрия, играющая столь важную роль в природе, универсальнее не только всех межэлементных отношений, которые описываются алгебраическими структурами, начиная с абелевой группы и ниже, но и такими еще более сложными отношениями, которые присущи различного рода пространствам.

2.5.0. Если в бесконечном множестве межэлементных отношений инвариантными оказываются такие структуры, которые упорядочены в пространственно-временной композиции, то для эмпирического и теоретического уровня нашего познания эти структуры существуют как материя. Материя, таким образом, — это то, чем одни элементы целостности становятся для других элементов, когда между ними возникают границы, а их отношения образуют композиции, которым присуща пространственно-временная упорядоченность.

Здесь, наверно, будет уместно сказать, чем, прежде всего, отличаются мои взгляды от ортодоксально материалистических.

Материалисты, признавая реальное, действительное бытие материи, утверждают, что она «…не существует иначе, как только в бесчисленном множестве конкретных форм структурной организации, каждая из которых обладает многообразием свойств и взаимодействий, сложным строением и является элементом некоторой, более общей системы». [10, с. 235]. Дальше этого материалисты не идут. Я же продолжаю и говорю, что самой общей системой или, если хотите, — сверхсистемой является Мир в целом, который именно как целостность, обладает только ему присущими интегральными свойствами; таких свойств нет и быть не может у его элементов. Эти системные, интегральные свойства Мира есть его сущность, а все остальное — это только моменты ее реализации.

В тезисе, к которому относятся эти замечания, делается попытка определить материю, исходя из такого понимания Мира. Я говорю, что материя — это то, чем одни элементы Мира становятся для других элементов, когда между ними возникают те или иные отношения, порождающие границы; и здесь не может быть речи о каком-либо субъективистском толковании материи. Скорее классическое противопоставление ее сознанию бросает на нее такую тень, ибо определять материю через сознание — значит, устанавливать, пусть даже негативную, но все же зависимость ее от сознания.

Итак, материя, это, прежде всего, межэлементные отношения, а в сфере этих отношений только то, что одни элементы представляют собою для других элементов. Такое истолкование материи освобождает ее от абсолютизации — она лишь один из возможных аспектов Мира. А принцип несводимости системы к ее элементам — это и есть творческое начало Мира.

В определении материи, которое сформулировано в тезисе 2.5.0, содержится еще одно условие, ограничивающее предмет определения — там говорится, что межэлементным отношениям для того, чтобы приобрести им статус материи, должна быть присуща пространственно-временная упорядоченность. Принципиально, Мир может быть и неупорядоченной системой или системой, которая упорядочена каким-либо другим образом. Возможно, что сингулярное состояние Вселенной, когда она, по нашим сегодняшним представлениям, имела огромную плотность, а пространство-время — огромную кривизну — так что все стягивалось как бы в одну точку, — возможно, что такое состояние Вселенной знаменовало собой переход от одного вида упорядоченности межэлементных отношений — к другому. Но это замечание я делаю между прочим и главным образом для того, чтобы показать эвристическое начало и потенциальную широту новой точки зрения.

2.6.0. Из сказанного с необходимостью следует, что отождествлять Мир и материю нельзя: Мир — всеобъемлющее единство всех принадлежащих ему элементов (функций, состояний) и всех четырех типов отношений, существующих в системе Мира; материя — это только один тип отношений — межэлементные, а внутри межэлементных отношений только такие, для которых инвариантны пространственно-временные композиции. К этому можно добавить следующее: если пространственно-временная упорядоченность межэлементных отношений является обязательным условием существования материи, то материя начинается там и тогда, где и когда появляются такие композиции. Все, что лежит за их пределами, или точнее, все, что предшествует по своей структуре и ее сложности пространственно-временным композициям, — все это существует, но еще не стало материей. Оно может стать материей, но для этого межэлементные отношения должны достичь определенной, высокой степени сложности, породить пространства (см. определение, например, векторного пространства).

2.7.0. Если все принадлежит Миру, то его обогащение может происходить только за счет конструирования новых элементов из уже имеющихся; математическую модель такого обогащения дает нам множество всех подмножеств. Обязательным элементом множества всех подмножеств, является пустое множество — ничто, которое оказывается, таким образом, конструктивным нечто в системе следующего, высшего иерархического уровня. В небытие уходит элемент только данного уровня, на другом уровне этот процесс может быть порождением. Но Мир в целом, как множество всех его подмножеств, есть система, элементами которой является бытие и небытие. Поэтому неправомерно ставить вопрос о существовании самой сущности Мира, всеобщего единства его элементов: — небытие лишь один из его элементов, в пределах одного или другого иерархического уровня. Мир же в целом есть единство бытия и небытия.

Н. Бурбаки так определяют множество всех подмножеств: «Множеством всех подмножеств множества ? называют множество (?), элементами которого служат все подмножества множества ?. Имеем ? ?(?), ??(?), и, каково бы ни было x??, {x}?(?)» [3, 267]. Проиллюстрируем это определение примером. Пусть произвольное множество ? будет содержать только два элемента

? = (a, b)

тогда множеством всех его подмножеств окажется (?), которое будет состоять из 2n элементов, где n — число элементов множества ?, в данном случае n=2. Тогда (?) будет:

(?) = {?},{a},{b},{a b}.

Если же мы пожелаем продолжить процесс обогащения первоначального множества и будем исходить теперь уже из множества всех его подмножеств, т. е. из (?), то получим следующую, уже значительно более сложную конструкцию из 24 элементов, а именно:

(?) = {?}, {?}, {a}, {b}, {a b}, {? a}, {? b},{? a b}, {a b}, {a {a b}}, {b {a b}},

{?, a, b}, {a, b, {a b}}, {?, a, b, {a b}}, {b, {a b}, ?}, {{a b}, ?, b}

Усложнение может быть продолжено до бесконечности. Так в множестве всех подмножеств только что приведенного множества будет уже 216 элементов, а в следующем 265 536 элементов и т. д. Среди всех этих элементов обращают на себя внимание те, которые являются сами по себе пустыми множествами ? и которых, с усложнением системы, становится все больше. В пределе это бесконечное множество имеет ту же мощность, какую имеет и бесконечное множество всех элементов самообогощающейся системы Мира.

Мир — это единство бытия и небытия. Но есть еще одно обстоятельство, которое должно задержать нас на этой теме: таким обстоятельством является так называемая «дурная бесконечность», форму которой приобретает обогащение системы за счет конструирования ее новых элементов из уже имеющихся. Мы можем без конца усложнять такую систему путем перехода от множества к множеству всех его подмножеств, но каждый раз перед нами оказывается нечто конечное. Бесконечно только все новое и новое усложнение и рост числа элементов. Спрашивается: так неужели Мир обречен пребывать в тенетах «дурной бесконечности» и ему никогда не суждено из них вырваться? Обречен на это не Мир, как целостность, а только один его аспект — аспект межэлементных отношений, который и есть не что иное, как бесконечное множество конечных отношений. Подлинная же бесконечность Мира в несоизмеримости его межэлементных отношений с отношениями этих элементов в целом. Но «дурная бесконечность» как последовательное повторение конечного, становящегося все более и более сложным, само по себе есть упорядоченное множество, где исходное множество ? предшествует множеству всех его подмножеств ?(?), а ?(?) принятое за новое исходное множество, предшествует ?(?1) и так далее до бесконечности:

? ? ?(?) ? ?(?1) ? … ? ?(??).

Такое множество, упорядоченное по принципу предшествования и возрастающего усложнения, представляет собою модель развития систем элементов во времени.

2.8.0. Когда межэлементные отношения из состояния «в себе» переходят в состояние «для себя», возникает рациональное познание, которое, достигнув определенного уровня и степени зрелости, становится наукой. Итак, наука есть рефлексия межэлементных отношений. Границы же научного познания определены его природой — сферой межэлементных отношений и их особенностями. И хотя наука — или лучше сказать — философия науки — это область самостоятельного исследования, которая далеко выходит за рамки настоящих тезисов, здесь все же надо сказать о том, что она не может быть единственным источником мировоззрения людей: при всей достоверности ее утверждений, она всегда была и будет отмечена неполнотой; кроме того, науке присущ моральный индифферентизм.

Но если наука — это рефлексия межэлементных отношений, то рассуждать научно можно только в пределах этих отношений. Даже тогда, когда предметом научного исследования становятся системы, элементами которых мы сами являемся (человеческое общество, ноосфера, Вселенная), научно мы изучаем их только опосредствовано — через принадлежащие им и противостоящие нам элементы, их сочетания и отношения. Наши непосредственные отношения к таким системам как к единому целому не могут быть областью научного исследования — это другая сфера, о которой речь пойдет впереди. Итак, если утверждения науки истинны (а в этом мы не сомневаемся), то не следует все же думать, что они содержат в себе всю истину, даже в пределах одной какой-либо проблемы. Науке, как уже сказано, присуща неполнота: Евклидова геометрия — одна из возможных геометрий, Ньютонова механика — одна из возможных механик. Когда на базе механики Ньютона было воздвигнуто здание механического мировоззрения — это была философия, основанная на науке своего времени, и в то же время это была философия, не способная удовлетворить нужды человеческого духа и объяснить Мир. В заслугу науке ставится ее объективизм. Действительно, он вполне соответствует природе межэлементных отношений, где каждый элемент противостоит всем остальным. Но объективизм выделяет только одну сторону, один тип отношений, только тот, который порождает между элементами границы. Другой тип отношений, тот, который основывается на принадлежности элементов целостности, на их единстве — остается вне поля его зрения.

Данный текст является ознакомительным фрагментом.