Глава 2. Архимед-физик

Глава 2. Архимед-физик

Архимеда справедливо считают основоположником математической физики. С его именем связывается введение понятия центра тяжести, открытие законов рычага и разработка основ гидростатики. Известно, что он занимался и геометрической оптикой, хотя его работы в этой области до нас не дошли. Для древних греков физика была целостным учением о мире и считалась частью философии. Ее практические стороны, такие, как механика, относились к прикладным дисциплинам. Математика хотя и применялась, но от нее не требовали ни строгости, ни полноты описания явлений.

Архимед первым подошел к решению физических задач с широким применением математики. Как уже говорилось, он начал с механики. Античные механические представления настолько отличались от наших, что сейчас воспринимаются с трудом, хотя «Физику» Аристотеля (384…322 г. до н. э.) в течение многих столетий изучали, комментировали, считали безошибочной. Аристотель разделял движения на «естественные» и «насильственные». Естественным считалось стремление материи к своему «месту», зависящему от ее свойств, например стремление камня к центру; Земли, огня — от Земли вверх. Насильственные движения предполагали внешнюю причину — приложение силы. Механика Аристотеля не знала явления инерции: движение должно было прекратиться тотчас же после прекращения действия силы. Движение же по инерции объяснялось влиянием среды. Так, последователи Аристотеля считали, что при бросании камня возникает воздушный вихрь, несущий его после того, как камень покинул руку.

В своих трудах Архимед изучал только силы, которые с точки зрения аристотелевой механики вызывают «естественные» движения. Более того, он сразу упростил задачу, исключив из нее движение. Так появилась статика.

До Архимеда закон рычага рассматривался в сочинении «Механические проблемы», автором которого долгое время считался Аристотель.

В «Механических проблемах», которые составлены в форме вопросов и ответов, содержится описание ряда инструментов и механизмов (рычаг, колодезный журавль с противовесом, клещи, кривошип, полиспаст, зубчатые колеса, рычажные весы) и объяснение их действия на основе «принципа рычага» и правила: «Выигрываем в скорости (пути) — проигрываем в силе».

Однако отсутствие ясности в постановке задач в ряде случаев приводило к совершенно неправильным представлениям. Вот как, например, описывается в «Проблемах» работа корабельного руля: «Почему малый руль, привешенный на корме корабля, имеет столь большую силу?..

Быть может, потому, что руль есть рычаг, а рулевой есть то, что приводит его в действие? Стало быть, место, где он прикреплен к кораблю, становится точкой опоры, руль в целом — рычагом, море — грузом, а рулевой — движущей силой». Действие руля, основанное на силе реакции отталкиваемой им воды, разумеется, нельзя свести к простому рычагу.

Нечетким рассуждениям, содержавшимся в «Механических проблемах», Архимед противопоставил безупречную теорию, построенную по законам геометрии. Архимед сделал в механике то, что греческие геометры сделали в египетской и вавилонской землемерной науке. Вместо полей они рассматривали отрезки плоскостей, вместо межевых границ — бесконечно тонкие и абсолютно прямые (или имеющие строго обусловленную кривизну) линии. И тогда оказалось возможным найти между фигурами соотношения, о которых не подозревала восточная математика, удовлетворявшаяся решением практических задач.

Архимед придал геометрическим фигурам вес, равномерно распределенный по площади или объему. В отличие от автора «Механических проблем» он рассматривает не реальные рычаги или барабаны, а их идеализированные схемы. Это тем более замечательно, что Архимед был и блестящим практиком-конструктором.

Из механических, вернее, механогеометрических сочинений Архимеда до нас дошли только два: «О равновесии плоских фигур» и «Эфод, или послание Эратосфену о механических теоремах». Однако отрывки из его более ранних механических сочинений «О весах» и «О рычагах» сохранились в произведениях ряда авторов. Наиболее важные из них, относящиеся к учению о центре тяжести, имеются в «Механике» александрийского ученого I в. н. э. Герона и в «Математической библиотеке» ученого III в. н. э. (также александрийца) Паппа.

Центр тяжести

Первым открытием Архимеда в механике было введение понятия центра тяжести, т. е. доказательство того, что в любом теле есть единственная точка, в которой можно сосредоточить его вес, не нарушив равновесного состояния.

Герон и Папп приводят со ссылкой на Архимеда доказательство существования центра тяжести. Герон предваряет теорему фразой, относящейся к рассмотрению Архимедом идеализированных «физико-математических» тел (метод абстракции). Герон пишет: «Никто не отрицает, что о наклонении и отклонении в действительности говорят только о телах. Если же мы говорим о плоских или телесных (объемных) фигурах, что некоторая точка является их центром поворота и центром тяжести, то это достаточно разъяснено Архимедом». Эта фраза подтверждает, что замена тел их теоретическими моделями была в науке новшеством, введенным Архимедом.

Архимедовы определение центра тяжести и теорему о его существовании мы приведем в пересказе Паппа.

Определение центра тяжести формулируется так: «…центром тяжести некоторого тела является некоторая расположенная внутри него точка, обладающая тем свойством, что если за нее мысленно подвесить тяжелое тело, то оно останется в покое и сохранит первоначальное положение».

Доказательство существования центра тяжести также основано на мысленном уравновешивании тела. В нем тело мысленно помещают на горизонтальную прямую, являющуюся основанием вертикальной плоскости (рис. 1): «Если какое-нибудь обладающее весом тело положить на прямую CD так, чтобы оно полностью рассекалось продолжением упомянутой плоскости, то оно может иногда занять такое положение, что будет оставаться в покое… Если затем переставить груз так, чтобы он касался прямой CD другой своей частью, то можно при поворачивании дать ему такое положение, что он, будучи отпущен, останется в покое… Если снова вообразить плоскость ABCD продолженной, то она разделит груз на две взаимно уравновешивающиеся части и пересечется с первой плоскостью… Если бы эти плоскости не пересеклись, то те же самые части были бы и уравновешивающимися и неуравновешивающимися, что нелепо».

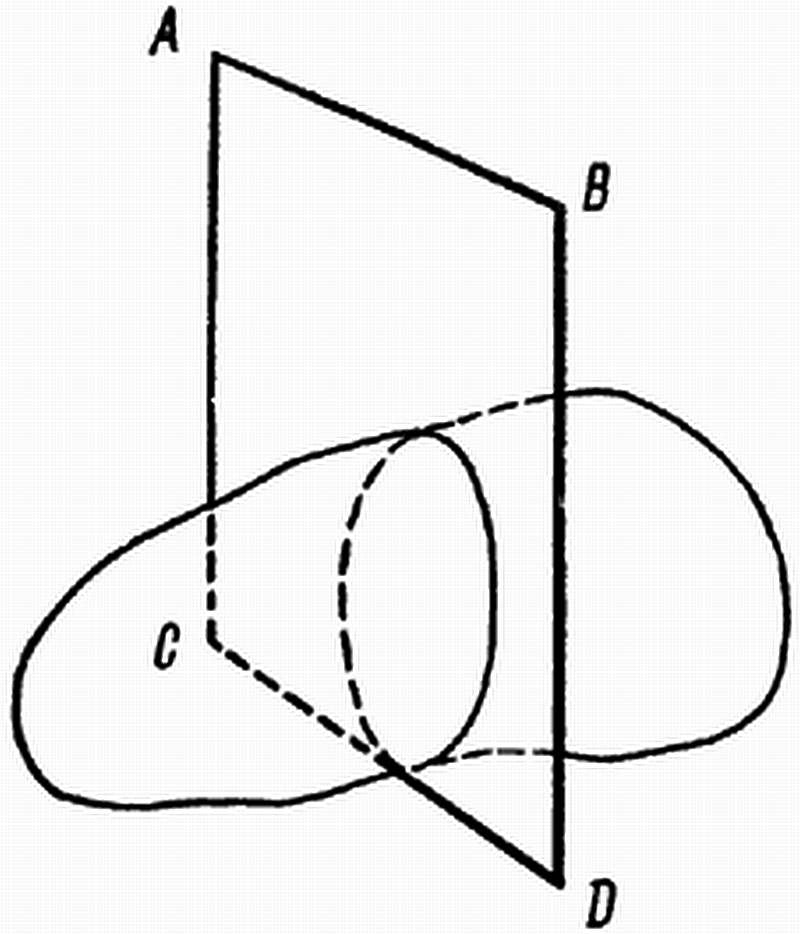
Рис. 1. К определению центра тяжести тела

Действительно, если бы плоскости, рассекающие груз на уравновешенные части, оказались параллельными (не пересекались), то можно было бы уравновесить тело, не поворачивая его, а только сдвинув параллельно самому себе. Это означало бы, что к одной из частей добавился бы отнятый от второй части объем, заключенный между плоскостями, что должно было бы нарушить равновесие. Путем подобных же рассуждений доказывается, что на линии пересечения плоскостей находится единственная точка, являющаяся центром тяжести.

Архимед решил ряд задач на нахождение центров тяжести различных геометрических фигур: треугольника, параллелограмма, конуса, сегмента параболы.

Закон рычага

Закон рычага, вероятно, был сформулирован в одном из упомянутых выше не дошедших до нас сочинений Архимеда. Причем сохранившийся в «Механике» Герона отрывок из сочинения Архимеда показывает, что в этом сочинении рассматривался случай, когда точки приложения сил расположены на окружностях разного диаметра, имеющих общую точку поворота. Это схема таких механизмов, как ворот, зубчатая передача и амфирион (разновидность ворота, состоящая из сидящих на одном валу барабанов разного диаметра). Приведя теорему, сводящую этот случай к рычагу, Герон пишет: «Это доказал Архимед в своей книге о равновесии. Отсюда ясно, что можно сдвинуть большую величину малой силой».

Но более серьезную разработку этих проблем Архимед предпринял позже в сочинении «О равновесии плоских фигур», состоящем из двух частей. В первой приводится ряд аксиом и теорем общего характера, а во второй с их помощью решается задача о нахождении центра тяжести сегмента параболы. В этой работе Архимед впервые развил аксиоматический подход к механике. Он строит свою теорию на базе геометрии путем добавления к геометрическим аксиомам нескольких «механических» аксиом. Книга начинается так:

«Сделаем следующие допущения:

1. Равные тяжести на равных длинах уравновешиваются, на неравных же длинах не уравновешиваются, но перевешивают тяжести на большей длине.

2. Если при равновесии тяжестей на каких-нибудь длинах к одной из тяжестей будет чтонибудь прибавлено, то они не будут уравновешиваться, но перевесит та тяжесть, к которой будет прибавлено».

Архимед приводит семь аксиом и на их основании доказывает ряд теорем, касающихся определения общего центра тяжести двух или нескольких фигур. Нахождение общего центра тяжести фигур сводится к их уравновешиванию на воображаемом рычаге, поскольку такое уравновешивание произойдет, если точка подвеса окажется в этом центре.

Содержание закона рычага, выведенного из аксиом, заключено в следующих двух теоремах:

1. «Соизмеримые величины уравновешиваются на длинах, которые будут обратно пропорциональны тяжестям».

2. «Если величины несоизмеримы, то они точно так же уравновешиваются на длинах, которые обратно пропорциональны этим величинам».

Разумеется, для практики, когда требуются лишь приближенные расчеты, вторая теорема не нужна. Но она имеет глубокий теоретический смысл, показывая, что закон рычага действует при любых отношениях плеч, включая и иррациональные.

Архимед не только ввел в геометрию новый класс задач (определение центров тяжести фигур), но и впервые применил при их решении «механические» методы (например, мысленное взвешивание для нахождения площадей сложных фигур).

Применив математику для изучения механического равновесия, Архимед показал, что математический подход к решению физических проблем не только помогает проникнуть в суть законов природы, но обогащает и саму математику.

«То механическое открытие»

В XI главе «Математической библиотеки» Паппа говорится: «Как определенный груз привести в движение определенной силой — это то механическое открытие Архимеда, которое заставило его радостно воскликнуть: «Дай мне место, где бы я мог стоять, и я подниму Землю!»

Сходный по содержанию текст имеется у Плутарха, который рассказывает: «Архимед, между прочим, писал однажды своему родственнику и другу царю Гиерону, что данной силой можно поднять любую тяжесть. В юношески смелом доверии к силе своего доказательства он сказал, что, если бы у него была другая Земля, он перешел бы на нее и сдвинул с места нашу. Удивленный Гиерон стал просить его доказать свои слова и привести в движение какое-либо большое тело малой силой. Архимед приказал посадить на царскую грузовую триеру, с громадным трудом с помощью многих рук вытащенную на берег, большой экипаж, положить на нее обыкновенный груз и, усевшись на некотором расстоянии, без всяких усилий, спокойно двигая рукой конец полиспаста, стал тянуть к себе триеру так тихо и ровно, как будто она плыла по морю».

Таким образом, открытие связывается с эффектной механической демонстрацией и со знаменитой фразой Архимеда о том, что он смог бы сдвинуть саму Землю. Обычно эту фразу относят к открытию закона рычага. Но рычаг был известен с незапамятных времен, а закон его действия, хотя и не строго, уже был сформулирован в «Механических проблемах». Кроме того, при попытке сдвинуть рычагом очень большой груз, мы получим весьма малое перемещение. Также мало вероятно, чтобы эта фраза относилась к какому-нибудь изобретенному Архимедом механизму, например винту. Ведь Папп говорит о каком-то открытом Архимедом законе, «как определенный груз привести в движение определенной силой». Ссылаясь на книгу Герона «Барулк», Папп пишет: «В «Барулк» он описывает, как поднять определенный груз определенной силой, причем он принимает отношение диаметра колеса к диаметру оси равным 5:1, предварительно допустив, что подлежащий поднятию груз весит 1000 талантов (25 т), а движущая сила равна 5 талантам (125 кг)». Далее Папп, меняя условия задачи (поднять груз в 160 талантов силой 4 таланта), описывает расчет многоступенчатого зубчатого редуктора, имеющего на входе червячную передачу. Слово «барулк», видимо, и является названием описываемого механизма.

«Открытие» не названо, но по крайней мере теперь мы знаем, что оно заключено в механизме, который мы бы назвали лебедкой, содержащей барабан для наматывания каната, несколько зубчатых передач и червячную пару. Кроме червячной передачи, которая входит в состав лебедки, остальные механизмы — ворот и зубчатые колеса — упоминаются в «Механических проблемах» и, значит, были известны до Архимеда.

Новым здесь был сам принцип построения многоступенчатой передачи. Открытие Архимеда должно было состоять в нахождении закона определения общего «выигрыша в силе», достигаемого с помощью механизма, состоящего из последовательно соединенных передач. Этот закон можно сформулировать так: общее передаточное отношение многозвенного механизма равно произведению передаточных отношений его звеньев.

Но это простое правило приводит к ошеломляющим результатам. Если взять пару зубчатых колес с отношениями радиусов 1:5 (как у Герона), то получим на большом колесе «выигрыш в силе» в 5 раз. Если же мы на вал с малым колесом насадим еще одно такое же большое и сцепим его с еще одним таким же маленьким, то получится уже «выигрыш» в 25 раз. Для редуктора с тремя такими передачами он будет равен 125, с пятью — 3125, а с семью передачами составит 390 625; наконец, взяв всего 12 передач, получим астрономическое число 1 220 703 125!

Найдя этот закон, Архимед открыл, на что способна механика, и счел не лишним продемонстрировать ее могущество окружающим.

Гидростатика

Хотя, как мы видим, Архимед ввел понятие центра тяжести и нашел закон рычага, в физику под именем закона Архимеда и архимедовой силы вошли понятия из его замечательного сочинения «О плавающих телах». Как и сочинение «О равновесии плоских фигур», это сочинение состоит из двух частей: вступительной, в которой даются основные положения, и основной, посвященной рассмотрению равновесия плавающего в жидкости параболоида вращения.

Замечательно, что роль аксиомы здесь берет на себя физическая модель «идеальной жидкости». «Предположим, — пишет Архимед, — что жидкость имеет такую природу, что из ее частиц, расположенных на одинаковом уровне и прилежащих друг к другу, менее сдавленные выталкиваются более сдавленными и что каждая из частиц сдавливается жидкостью, находящейся над ней по отвесу, если только жидкость не заключена в каком-нибудь сосуде и не сдавливается чем-нибудь другим». Это единственное предположение, исходя из которого Архимед выводит все остальное.

Первым выводом является доказательство того, что «поверхность всякой жидкости, установившейся неподвижно, будет иметь форму шара, центр которого совпадает с центром Земли».

Далее следуют теоремы: «Тела, равнотяжелые с жидкостью, будучи опущены в эту жидкость, погружаются так, что никакая их часть не выступает над поверхностью жидкости и не будут двигаться вниз», «Тело, более легкое, чем жидкость, будучи опущено в эту жидкость, погружается настолько, чтобы объем жидкости, соответствующий погружений части тела, имел вес, равный весу всего тела», Тела, более легкие, чем жидкость, опущенные в эту жидкость насильственно, будут выталкиваться вверх силой, равной тому весу, на который жидкость, имеющая равный объем с телом, будет тяжелее этого тела», «Тела, более тяжелые, чем жидкость, опущенные в жидкость, будут погружаться, пока не дойдут до самого низа, и в жидкости станут легче на величину а жидкости в объеме, равном объему погруженного тела».

Трудно представить себе более ясные и четкие формулировки поведения в воде плавающих тел. Но возникает вопрос: правомочно ли было выводить их из принятого вначале положения о свойствах жидкости. Как можно доказать его правильность?

И тут мы впервые в истории физики встречаемся со своеобразием ее аксиом.

Архимед предлагает нам мысленно представить себе вещество, состоящее из абсолютно скользких атомов, способных передавать давление во все стороны и подвергающихся давлению со стороны таких же атомов, находящихся сверху. Потом он математически исследует это вещество. Оказывается, что поверхность такого вещества в свободном состоянии есть сфера с центром в центре земного шара. Но так как это общеизвестный факт (форма поверхности Мирового океана), то отсюда можно сделать обратный вывод: поскольку поверхность океана — сфера, то жидкость имеет именно такое строение, какое постулировано Архимедом. Можно также не сомневаться в том, что выведенные математические законы гидростатики Архимед проверял на опыте.

Таким образом, сочинение «О плавающих телах» — первая попытка экспериментально проверить фундаментальное предположение о строении вещества путем создания его модели. В этом сочинении Архимед не только подтвердил атомистические идеи Демокрита, но и доказал ряд важных положений о физических свойствах атомов жидкости.

Архимед вывел законы гидростатики для идеальной жидкости, описав ее свойства. Свойства реальной жидкости немного отличаются от свойств архимедовой идеальной жидкости. Эти отличия в некоторых случаях играют заметную роль. Так, вопреки законам Архимеда смазанная жиром иголка может держаться на поверхности налитой в сосуд воды. Но нельзя упрекнуть ученого в неверности его законов. Эти законы справедливы постольку, поскольку жидкость приближается к идеальной модели. Для описания свойств реальной жидкости надо внести соответствующие поправки в модель. Но это не опровергает справедливость выкладок Архимеда.

Определение удельного веса

Римский архитектор Витрувий, сообщая о поразивших его открытиях разных ученых, приводит следующую историю: «Что касается Архимеда, то изо всех его многочисленных и разнообразных открытий то открытие, о котором я расскажу, представляется мне сделанным с безграничным остроумием.

Во время своего царствования в Сиракузах Гиерон после благополучного окончания всех своих мероприятий дал обет пожертвовать в какой-то храм золотую корону бессмертным богам.

Он условился с мастером о большой цене за работу и дал ему нужное по весу количество золота. В назначенный день мастер принес свою работу царю, который нашел ее отлично исполненной; после взвешивания корона оказалась соответствующей выданному весу золота.

После этого был сделан донос, что из короны была взята часть золота и вместо него примешано такое же количество серебра. Гиерон разгневался на то, что его провели, и, не находя способа уличить это воровство, попросил Архимеда хорошенько подумать об этом. Тот, погруженный в думы по этому вопросу, как-то случайно пришел в баню и там, опустившись в ванну, заметил, что из нее вытекает такое количество воды, каков объем его тела, погруженного в ванну.

Выяснив себе ценность этого факта, он, не долго думая, выскочил с радостью из ванны, пошел домой голым и громким голосом сообщал всем, что он нашел то, что искал. Он бежал и кричал одно и то же по-гречески: «Эврика, эврика! (Нашел, нашел!)».

Затем, исходя из своего открытия, он, говорят, сделал два слитка, каждый такого же веса, какого была корона, один из золота, другой из серебра. Сделав это, он наполнил сосуд до самых краев и опустил в него серебряный слиток, и… соответственное ему количество воды вытекло.

Вынув слиток, он долил в сосуд такое же количество воды… отмеряя вливаемую воду секстарием (0,547л), чтобы, как прежде, сосуд был наполнен водой до самых краев. Так он нашел, какой вес серебра соответствует какому определенному объему воды.

Произведя такое исследование, он таким же образом опустил золотой слиток… и, добавив той же меркой вылившееся количество воды, нашел на основании меньшего количества секстантов воды (секстант — римская мера веса, равная 0,534 Н), насколько меньший объем занимает слиток».

Потом тем же методом был определен объем короны. Она вытеснила воды больше, чем золотой слиток, и кража была доказана.

Часто этот, рассказ связывают с открытием закона Архимеда, хотя он касается способа определения объема тел неправильной формы.

Возможно, что в этом рассказе Витрувия ванна, забытая одежда и возглас «Эврика!» являются вымыслом, но нас интересуют научные факты. Во-первых, бросается в глаза, что согласно описанию Витрувия Архимед сделал больше того, что требовалось. Чтобы обнаружить примесь, достаточно было сравнить объем короны с объемом равного ей веса золота. По-видимому, Витрувий не вполне разобрался в какой-то другой принадлежавшей Архимеду задаче об определении удельного веса тел. Об этом свидетельствует и фраза: «Отсюда он нашел, какой вес серебра соответствует какому объему воды». В ней, собственно, и содержится определение удельного веса — отношение веса к объему или к весу вытесненной воды (при измерении объема золотого слитка говорится о весе воды).

Таким образом, Архимед является автором методики определения удельного веса тел путем измерения их объема погружением в жидкость.

Оптика

В своем стремлении математически описать явления природы Архимед выделял задачи, наиболее поддающиеся геометрическому анализу. Поэтому занятия Архимеда в области геометрической оптики — «катоптрике», как ее называли прежде, можно считать закономерными.

Очень немного можно сказать о «катоптрике» Архимеда. От нее в позднем пересказе уцелела единственная теорема, в которой доказывается, что при отражении света от зеркала угол падения луча равен углу отражения. Свои оптические теории (как и механические) Архимед строил на основе аксиом. Одной из таких аксиом являлась обратимость хода луча — глаз и объект наблюдения можно поменять местами. Весь же круг вопросов «катоптрики» был очень широк.

Перечисление проблем, которых касался Архимед в этой книге, мы находим у других авторов античного периода. Вот как об этих работах говорил Апулей: «Почему в плоских зеркалах предметы сохраняют свою натуральную величину, в выпуклых — уменьшаются, а в вогнутых — увеличиваются; почему левые части предметов видны справа и наоборот; когда изображение в зеркале исчезает и когда появляется; почему вогнутые зеркала, будучи поставлены против Солнца, зажигают поднесенный к ним трут; почему в небе видна радуга; почему иногда кажется, что на небе два одинаковых Солнца, и много другого подобного же рода, о чем рассказывается в объемистом томе Архимеда». Из других свидетельств следует, что Архимед изучал также и явление преломления лучей в воде.

С «катоптрикой» связана легенда о поджоге Архимедом римских кораблей во время осады Сиракуз. Что в ней вымысел и что, быть может, является отражением действительных событий, мы рассмотрим в отдельной главе.

Можно не сомневаться в том, что «катоптрика» Архимеда оказала большое влияние на последующее развитие оптики.

Влияние работ Архимеда на развитие физики

Если говорить об ученых, опередивших свое время, то Архимед, вероятно, может считаться своеобразным рекордсменом. Его идеи нашли продолжателей лишь через 1800 лет.

Предложенное Архимедом направление в науке — математическая физика, которую он провозгласил и в которой так много сделал, не была воспринята ни его ближайшими потомками, ни учеными средневековья.

Архимеда знали как гениального математика, им восхищались, его изучали и комментировали, но его физические работы долгое время не получали развития.

В какой-то мере в средние века на сочинениях Архимеда базировались работы ряда ученых Востока о взвешивании и определении удельного веса веществ. Математик и астроном IX в.

Сабит ибн-Корра перевел на арабский язык и прокомментировал многие сочинения Архимеда и составил трактат о рычажных весах. На основе сочинения Архимеда «О плавающих телах» крупнейшие ученые того же времени ал-Бируни и Омар Хайям провели определения удельных весов большого количества металлов и драгоценных камней. При этом ал-Бируни пользовался методом сравнения значений веса равных объемов различных минералов, а Омар Хайям — методом взвешивания образцов на воздухе и в воде.

В эпоху Возрождения, когда центр научной мысли вновь переместился в Европу, европейская наука училась у арабской. Некоторые труды Архимеда дошли до нас только в арабских переводах. Одним из первых продолжателей механики Архимеда был итальянский ученый и инженер Гвидо Убальди дель Монте (1545…1607), исследовавший вопросы равновесия и решивший задачу о грузе на наклонной плоскости. Многое сделал для развития статики Архимеда другой итальянский ученый — Джовани Баттиста Бенедетти (1530…1590). Крупнейшим механиком «школы Архимеда» был фламандский ученый Симон Стевин (1548…1620). В своем классическом труде «Начала статики» он не только исходит из ряда аксиом Архимеда, но и развивает его работы, анализируя целый ряд механизмов. В число постулатов Стевин вводит принцип невозможности вечного двигателя; ему принадлежит также введение обозначений сил в виде стрелок. Много Стевин сделал и в области гидростатики, развив положения Архимеда, данные им в «Плавающих телах». Интерес Стевина к этим проблемам был далеко не абстрактным, так как он занимал должность инспектора плотин и консультанта голландского адмиралтейства.

Главным достижением классической механики была математическая разработка законов динамики Галилеем и Ньютоном. И хотя здесь достижения Архимеда непосредственно не использовались, его математический подход к проблемам торжествовал. Знаменательно, что Галилей хорошо знал труды Архимеда и часто к ним обращался. Например, при рассмотрении |равноускоренного движения он писал: «Я не предполагаю ничего иного, кроме определения движения; я хочу трактовать и рассматривать это явление в подражание Архимеду, который, заявив в «Спиральных линиях», что под движением по спирали он понимает движение, слагающееся из двух равномерных (одного — прямолинейного, а другого — кругового), непосредственно переходит к демонстрации выводов. Я заявляю о намерении исследовать признаки, присущие движению тела, начинающемуся с состоянии покоя и продолжающемуся с равномерно возрастающей скоростью, а именно так, что приращения этой скорости возрастают не скачками, а плавно, пропорционально времени».