КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
Настало теперь время пояснить, почему Фарадей, стоя наверху лестницы, весело крикнул Максвеллу, проталкивающемуся локтями через толпу:
— Послушайте, Максвелл! Уж вам-то, специалисту по движению молекул, сам бог велел легко пробираться в толпе!
Действительно, и в конце абердинского периода, и в начале лондонского у Максвелла появилось наряду с оптикой и электричеством новое научное увлечение — кинетическая теория газов. На занятия ею его натолкнули две статьи Клаузиуса 1857 и 1859 годов. В статьях рассматривалась роль, которую могла бы играть вращательная энергия молекул в теплосодержании вещества, и была сделана попытка определить физический смысл понятия свободного пробега молекулы.
Эти статьи давали новое развитие взглядам Даниила Бернулли, члена Петербургской академии наук.
Бернулли первым указал на то, что теплота есть внешнее проявление колебательного движения отдельных молекул. Молекулы, следовательно, обладали скоростью. Все — одинаковой. Клаузиус первый высказал мысль о том, что эти скорости могут быть разными.
Но разные скорости — это гигантская трудность в формулировании газовых законов. Ведь немыслимо записывать эти законы для каждой отдельной молекулы! И Клаузиус приходит к понятию «средней» скорости молекул, точнее — средней кинетической энергии молекул.
Клаузиус, сказав «а», не говорил «б».
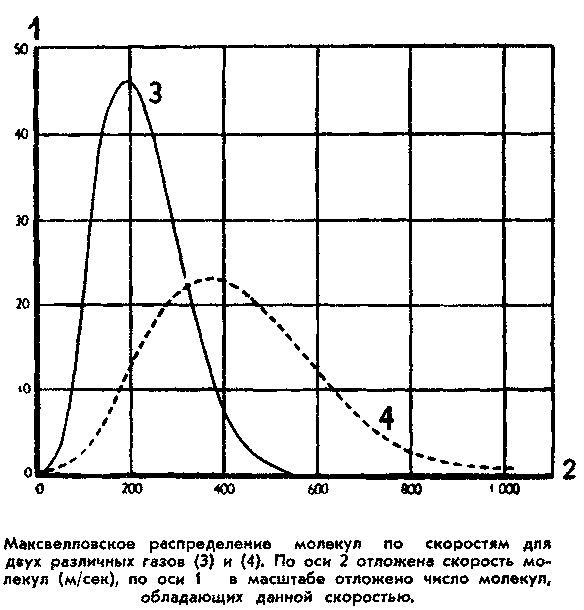
Можно ли переделать формулы кинетической теории таким образом, чтобы учесть различие между скоростями молекул, учесть каждую отдельную молекулу? Конечно, нельзя! Но всегда можно математически точно выразить, насколько вероятно существование в газе при определенной температуре молекул с именно такой скоростью и какую часть от общего числа будут составлять молекулы с такой скоростью или близкой к ней. Существовавшая уже к тому времени теория вероятностей позволяла, например, вычислить вероятность попадания пули в мишень или вероятность проживания, например, в Лондоне мужчин именно такого роста. Эта возможность — и попадания пули в мишень, и наличия в Лондоне людей такого-то роста, и наличие в газе молекул с такой-то скоростью — описывалась однотипной кривой, имеющей форму колокола. Вершина ее соответствовала и «яблочку» мишени, и самому что ни на есть часто встречающемуся мужскому росту в Лондоне того времени: 168 сантиметров, и наиболее вероятной в данном газе скорости молекулы.
Это было нововведением колоссальной, непреходящей, философской важности для физики. Впервые в физике были сказаны слова «вероятно», «это событие может произойти с большой степенью вероятности». Раньше события были строго детерминированы. Все физические законы несли на себе печать полной определенности.
Если известен путь и время равномерного прямолинейного движения, можно однозначно определить скорость, причем не с какой-либо степенью вероятности, а совершенно точно.
По Максвеллу, в результате взаимных столкновений между упругими шариками — молекулами газа — в конечном счете получается некоторое стационарное распределение скоростей, группирующихся при заданной температуре вокруг наиболее вероятной скорости. Могут быть люди очень высокого роста и очень низкого, но наиболее вероятным ростом мужчины в Лондоне в 1860 году будет именно 168 сантиметров, и эта цифра уже совсем не «вероятна», а абсолютно точна.
В физику впервые вошли вероятностные представления, законы статистики. В физике произошла революция, а многие слушатели докладов Максвелла на ежегодных встречах Британской ассоциации 1859 года в Абердине и затем в 1860 году в Оксфорде этого даже не заметили. Для большинства это было очередным физико-математическим упражнением, с помощью которого можно было прийти к тем же выводам, что и раньше, при принятии одной, средней скорости молекул в газе. Это, по мнению многих, было лишь математической гипотезой, не лучшей и не худшей, чем другие, поскольку результаты получались теми же, что и у Клаузиуса с его одной «среднеквадратичной» скоростью. А может быть, эта новая теория казалась кое-кому и вредной, поскольку молекулярный хаос, введенный Максвеллом, был внешне куда менее привлекателен и математически куда более сложен.
А один из выводов новой теории, не совпадавший со старыми, выведенными из предположения о равенстве скоростей молекул, был просто физически абсурден. И что самое смешное — сам докладчик тоже не верил в него, но так это получалось из теории. Молодой Максвелл предлагал кому угодно проверить его выкладки и найти в них ошибку, если она есть. И похоже, что он сам этого страстно желал — ошибки, поскольку ему самому вывод казался парадоксальным, физически неочевидным: получалось, что вязкость газа не зависела от его давления!
— Этот вывод из математической теории является крайне поразительным, — говорил молодой докладчик, — и единственный опыт, с которым я встретился в этой области, как будто его не подтверждает...
Неплохое заявление для автора новой теории! Эта теория не давала пока никаких особенно новых результатов, за исключением, как всем казалось, заведомо неверного, и отношение к ней было прохладным. А ряд ученых прямо заявили, что эта теория ненаучна, спекулятивна, поскольку истинная наука не должна иметь дела с «ненаблюдаемыми» величинами.
Максвелл и не заметил, как попал в самую горячую точку философских битв. Но здесь ему нечего было бояться — его крепкая философская позиция спасала его как от Сциллы идеализма, так и от Харибды механицизма.
Максвеллу удалось подчинить строгим законам хаотическое движение молекул газа. Именно полная беспорядочность движения молекул позволила ему извлечь из хаоса порядок. Статистический, вероятный подход позволял точно указать, например, число частиц, обладающих удвоенной или утроенной средней кинетической энергией. И эти цифры, как оказалось, подчинились универсальному закону, который не зависит от природы частиц и сил, с которыми они действуют друг на друга. В каком-то смысле закон распределения молекул по скоростям, данный Максвеллом, оказался новым фундаментальным свойством материи, находящейся в равновесии, свойством, не известным ранее никому. Максвелл подошел к самым границам механического понимания материи. И переступил их.
Да, Максвелл попал на линию огня, лучше сказать — на ничейную землю, обильно осыпаемую градом снарядов обеих враждующих сторон, двух групп философов. Вывод Максвелла о господстве в мире молекул законов теории вероятностей затрагивал самые фундаментальные основы мировоззрения, и противники, найдя наконец общего врага, объединились в атаках на него.
Одни полагали, что все в природе может быть объяснено на основе механических представлений. Некогда ценное, но возведенное в XIX веке в абсолют, такое мнение привело в конце концов к грубому механицизму, убеждению в том, что движущей силой мира являются законы механики, с помощью которых можно объяснить любые явления.
Очевидная несостоятельность такой теории, невозможность объяснить многие вновь открытые закономерности чисто механическим путем (не один физик сломал зубы, пытаясь механически представить второй закон термодинамики!) привели к появлению другой теории — феноменологической. Сторонники ее призывали изучать мир таким, как он есть, упорядочивать и описывать опытные данные, не вдаваясь в «спекуляции», умствования, не строя никаких моделей, не подтвержденных опытом. Эти стали абсолютизировать уже опыт и ощущения. С ними Максвелл, столько времени потративший на теорию цветов, и убедившийся в крайней субъективности ощущений — сравните ощущения дальтоника и нормального человека! — никак не мог бы согласиться. Их с Максвеллом разделяла глубочайшая убежденность его в конечной познаваемости мира, в возможности объяснения даже самых сложных явлений.
Его материалистическое миропонимание, окрепшее в общении с природой, в изучении ее, его опыт, говорящий об объективности и познаваемости законов природы, несгибаемы. И в то же время не так прост он, Максвелл, чтобы соглашаться с механицистами, — изучение фарадеевских трудов, его собственные, находящиеся в зародыше электрические теории подсказывают ему, что не все так просто, как толкуют механицисты, фетишизирующие законы механики. Чего стоит хотя бы некритичное восприятие закона тяготения, пусть блестяще доказавшего правильность своей математической интерпретации в открытии Адамса и Леверрье! Даже закон тяготения, понимаемый как действие ни через что, просто через расстояние, неизбежно приводил к тому, что у тел появились некие «присущие им изначально» свойства притяжения, совершенно таинственным способом сообщаемые без посредства среды партнеру по взаимодействию.
Нет, не прост был молодой Максвелл, слишком искушен он был уже в математической физике, чтобы попасть в объятия механицистов. Да, он использует законы соударения упругих шариков, которыми он представляет молекулы, но считает ли он молекулы только упругими шариками? С другой стороны, Максвелл выступает против фетишизации субъективных ощущений, но разве не он же считает опыт высшим критерием правильности любой физической теории?
Обвиняли Максвелла в механицизме — мол, слишком увлекается средствами классической механики, механическими моделями... Обвиняли на этот раз несправедливо — Максвелл всегда считал, что механическая модель лишь в самых общих и простых чертах отражает исследуемые процессы и явления природы. Любой механический образ, по Максвеллу, отражает природу отнюдь не тождественно, а с определенной степенью приближения, отражает лишь одну сторону ее свойств. Механические модели, механические представления играли у Максвелла роль рабочих гипотез, конструкций, помогающих изобразить сложные предметы и явления гораздо проще и наглядней. Механические модели были строительными лесами его теорий.
Нельзя было ограничиваться чисто феноменологическим описанием. С другой стороны — невозможно было абсолютизировать и гипотетическое описание. Избрав середину, Максвелл пришел к методу аналогий, при котором можно было привлекать физические отношения в уже изученных явлениях и впервые учитывать данные, характеризующие новые явления. И поскольку из старых отраслей науки именно механика была наиболее разработанной, то механические аналогии, как самые наглядные, самые ясные и понятные, были вполне уместны и закономерны. И тут — главное. Механические модели были для Максвелла правомерны лишь до тех пор, пока они подтверждали то, что наблюдалось в экспериментах. Он был готов отказаться от своего вывода о независимости коэффициента внутреннего трения газов от давления, вывода математически безупречного, ввиду казавшегося тогда очевидным несовпадения этого вывода с экспериментом.
Будучи по складу своего мышления физиком, твердо уверенным в объективном и независимом от субъекта существовании окружающего мира, будучи уверенным во всеобщей взаимосвязи и изменчивости явлений, в их многоликости и «многослойности», Максвелл буквально на каждом шагу демонстрировал диалектичность своего мышления, и введение им совершенно немыслимых с позиций механицизма вероятностных, статистических методов в молекулярную теорию доказало зрелость его философских концепций, мощь философских обобщений. Заявление о том, что в мире молекул «господствует случай», было по своей смелости одним из величайших подвигов в науке.
Данный текст является ознакомительным фрагментом.