Глава 6 Ближние горизонты

Глава 6

Ближние горизонты

Проще просить прощения, нем разрешения.

Приписывается Грейс Хоппер, женщине-математику и военному моряку.

Подобное внимание приятно, но вызывает неловкость. Мне бы хотелось, чтобы меня запомнили как математика, по теоремам, которые я доказала, и по задачам, которые я решила.

Джулия Робинсон

Грейс Мюррей Хоппер (1906–1992)

Кто же главный герой этой главы? Контр-адмирал, получивший это звание в 1983 году, в возрасте 77 лет, или миноносец «Хоппер»? Конечно же, сам контр-адмирал — миноносец был назван в его честь. Но есть одна небольшая деталь: этот контр-адмирал был женщиной… Если мы добавим, что эта женщина была математиком, большим специалистом по компьютерам, а также, среди прочего, придумала язык программирования COBOL, то читатель посмотрит на нее совершенно другими глазами. Да, все эти и многие другие качества сочетала в себе Грейс Хоппер по прозвищу Изумительная Грейс (от англ. Amazing Grace — название одного из христианских гимнов).

Пушки и компьютеры

При рождении Грейс Хоппер получила имя Грейс Брюстер Мюррей. Она была правнучкой адмирала Джорджа Мюррея, который стал ее кумиром на всю жизнь. Сильный и независимый характер Грейс, должно быть, сформировался под влиянием родителей. Мать, Мэри Кэмпбелл ван Хорн, в юности также получила образование, но не справилась с давлением общества. Она бы с удовольствием занималась математикой, но это считалось неподходящим занятием для девушки. Отец, Уолтер Флетчер Мюррей, был страховым брокером, но когда его дети были еще совсем маленькими, из-за болезни кровеносной системы ему ампутировали одну за другой обе ноги. Несмотря на невзгоды, семья не сдавалась: Грейс получила образование, а ее отец дожил до семидесяти лет. Уолтер Мюррей воспитывал в детях уверенность в том, что усилием воли можно достичь всего. Кроме того, он не проводил различия между обучением девочек и мальчиков.

Грейс родилась в эпоху зарождения технологий: в воздух поднялся самолет братьев Райт, с конвейера сошел «Форд Т» Генри Форда. Когда Грейс было всего семь лет, она из любопытства разобрала домашние часы, чтобы узнать, как они работают. По всей видимости, ей не удалось сразу понять принцип действия часов, и она продолжила свои исследования. И только после того, как Грейс разобрала семь часов, мать заподозрила неладное и прекратила эти жертвоприношения. Возможно, именно поэтому на часах в офисе Грейс часовая стрелка двигалась в обратную сторону: это было еще одним проявлением инновационности и оригинальности мышления, которые Грейс так высоко ценила. Одно из ее изречений гласит: «Кораблю в порту ничто не угрожает, но он был построен не для этого. Выходите в открытое море и совершайте открытия».

Поступить с первой попытки в престижный Колледж Вассара Грейс не удалось, так как она не сдала экзамен по латыни (сегодня подобное невозможно). Она поступила со второй попытки и во время учебы получала высшие отметки по математике и физике. Позднее Грейс была присвоена степень доктора в Йельском университете, и она стала первой женщиной в истории, удостоенной такой чести. Ее научным руководителем был знаменитый алгебраист Ойстин Оре. Затем Колледж Вассара предложил девушке место преподавателя, а впоследствии и доцента. В 1941 году Грейс получила стипендию на обучение в Курантовском институте математических наук в Нью-Йорке — об этом заведении все отзывались с почтением и трепетом.

К тому времени Грейс уже вышла замуж за Винсента Хоппера, преподавателя иностранных языков Нью-Йоркского университета, и прожила в браке до конца войны. Когда в 1945 году супруги развелись, она сохранила фамилию мужа. В том же году ее уже бывший муж погиб на поле боя.

Подобно героям романов, которые слышат зов предков, в 1943 году Грейс услышала зов отечества. После бомбардировки Пёрл-Харбора Соединенные Штаты вступили в войну, и Грейс записалась добровольцем на флот, в знаменитые Военно-морские силы США. Это было непросто: ее вес был меньше минимально допустимого на целых семь килограммов, и ей пришлось добиваться исключения из правил. В итоге Грейс была принята в ряды ВМС и стала лучшей в своем выпуске. По окончании занятий в учебной части она получила звание младшего лейтенанта. Вышестоящие офицеры поступили весьма благоразумно, отправив Грейс исполнять приказы математика Говарда Эйкена (1900–1973) и его компьютера Mark I. О первом появлении Хоппер в лаборатории позднее ходили легенды. «Где, черт возьми, вы были? Коэффициенты для функции arctg х должны быть готовы к четвергу!» — закричал Эйкен, едва увидев ее. Впоследствии Хоппер и Эйкен написали множество совместных статей, посвященных не только Mark I, но и его следующим версиям — Mark II и Mark III. Чтобы подготовить любителей вычислений к работе с новым инструментом — компьютером, Грейс составила руководство объемом в 500 страниц.

Mark I, который, по мнению многих, был первым суперкомпьютером в истории, насчитывал свыше 15 метров в длину и 2,5 метра в ширину и высоту. Этот мастодонт, несмотря на свои размеры, обладал смехотворно малым объемом памяти и мог выполнять всего три операции сложения в секунду. Любой современный персональный компьютер посмотрел бы на него свысока! Такими были первые робкие шаги информатики.

Однако в те годы подобная скорость вычислений была невероятной, и передовые инструменты, способные ее обеспечить, предназначались исключительно для военных нужд, прежде всего для артиллерии. В бизнесе компьютеры начали использоваться позже. Компьютеры были тайной для всех, за исключением избранной касты специалистов. Как-то раз во время визита комиссии, состоявшей из нескольких адмиралов, проклятый компьютер то включался, то выключался, и Грейс спасла положение, небрежно положив палец на кнопку питания. Никто ничего не заметил.

Вверху — миноносец ВМС США «Хоппер». Внизу — контр-адмирал Грейс Хоппер в январе 1984 года. Грейс Хоппер — единственная женщина-математик, именем которой назван корабль.

* * *

В ВАШЕМ КОМПЬЮТЕРЕ ЗАВЕЛСЯ «БАГ»

Однажды, давным-давно, один компьютер постоянно совершал ошибки, и некоторые сомневались, что его программа правильно написана. Этим компьютером был Mark II, на дворе стоял 1947 год. После тщательного анализа оказалось, что причиной ошибок было обычное насекомое, застрявшее между контактами. Оно было обнаружено и «заархивировано», то есть вклеено в журнал происшествий. Так окончилась жизнь бедного насекомого — «бага» (по-английски bug означает «жук»). Хотя жука обнаружила не Г рейс, считается, что именно с ее легкой руки это слово вошло в обиход. С тех пор «баг» в программе обозначает уже не настоящего жука (сегодня это совершенно немыслимо), а ошибку в аппаратном или программном обеспечении. Ранее слово «баг» уже использовалось для обозначения неполадок в аппаратном обеспечении, и вот этот «жук» навсегда занял свое место в языке.

К компьютерным багам следует относиться со всей серьезностью. Они встречаются достаточно часто, обнаружить их порой очень сложно, и они могут нанести моральный и материальный ущерб на миллионы евро. Чтобы вы могли понять, как сложно бывает обнаружить баги, приведем всего один пример. Может случиться так, что несколько программ конфликтуют при выполнении единственной операции (это случается постоянно). Хотя по отдельности обе функционируют корректно, при одновременной работе обеих в неподходящий момент всегда возникает ошибка.

Некоторые происшествия, вызванные багами, весьма известны: в 1980-е годы баг в компьютерной программе медицинского оборудования привел к изменению дозы облучения при радиотерапии, что стало причиной смерти множества пациентов. Меньший резонанс среди широкой публики вызвал баг в управляющей программе прототипа ракеты «Ариан-5», ставший причиной падения ракеты. Цена этой ошибки составила 1 млрд долларов. По официальным оценкам американской комиссии, ежегодно в результате багов теряется 0,6 % валового национального продукта. Объявим же войну багам: эти мелкие ошибки могут нанести огромный ущерб.

Первый «баг» в истории, хранящийся в Национальном музее американской истории. В отличие от современных, этот «баг» был настоящим.

* * *

Взгляд в будущее

По окончании войны Грейс была зачислена в резерв ВМС. В течение всей жизни она постоянно занимала сразу несколько должностей. В 1949 году она также занялась делами частной компании, которая меняла названия: Remington, Sperry, Sperry-Rand и в конечном итоге получила название UNIVAC. Когда Грейс была принята на должность ведущего математика, компания называлась Eckert-Mauchly Corporation. Отметим, что Джон Преспер Экерт (1919–1995) и Джон Уильям Мокли (1907–1980), чьи имена носила компания, были создателями первого электронного многоцелевого компьютера, также имевшего огромные размеры, — легендарного ENIAC. Теперь они занимались не только военными задачами, связанными с баллистикой и взломом шифров, но и вопросами бизнеса. Информатика стала обычной наукой, и ее бурное развитие было уже не остановить.

В развитие информатики немалый вклад внесла Грейс Хоппер: она работала над компилятором, который со временем получил название FLOW-MATIC. 1952 год повсеместно считается годом рождения первого компилятора. Но сделаем небольшое отступление, чтобы объяснить, что это такое.

В информатике различают машинный язык, который, если можно так выразиться, понятен компьютеру, и язык программирования, который используют программисты. Машинный язык проще, чем языки программирования, так как машина «глупа», но выполняет действия быстро, а программист намного «умнее», но выполняет действия медленнее. Компиляция — крайне трудоемкий этап: его смысл заключается в том, чтобы изложить процесс, придуманный человеком, так, чтобы компьютер его понял. В 1950 году Грейс Хоппер предвидела, что программы в будущем станут дороже аппаратного обеспечения. Она отстаивала свою точку зрения вопреки всеобщему скепсису, и время подтвердило ее правоту.

Работа Грейс Хоппер над компиляторами имела неожиданный результат: так как в информатике правят бал байты, состоящие из восьми бит, ей пришлось научиться проводить расчеты в восьмеричной системе счисления. Грейс овладела этой наукой в совершенстве и часто выполняла в ней обычные расчеты, например стоимости покупок в магазине. Она забыла десятичную систему счисления, рискуя при этом личными финансами.

Любой другой удовольствовался бы тем, что создал столь ценную программу, как компилятор, позволяющий компьютерам выплачивать зарплату и формировать счета, но не такова была Грейс Хоппер. Компьютеры стали не просто машинами, способными быстро выполнять арифметические действия, — они умели «мыслить» на языке математики и понимать пользователей. Грейс совершила еще один шаг вперед: рассказывают, что ей было неудобно работать с чековой книжкой и банковским счетом, и она попыталась сделать так, чтобы машина «понимала» английский язык — язык самой Грейс, язык бизнеса и большинства пользователей. В 1956 году ей удалось добиться того, что UNIVAC при помощи ее компилятора «понял» два десятка команд на английском языке. Так началось развитие языка COBOL. Чтобы четко определить его стандарты, в 1959 году был создан специальный комитет.

В 1966 году в силу возраста Грейс Хоппер была вынуждена уйти в отставку из военно-морских сил. Но не стоит думать, что ее история на этом заканчивается. ВМС предприняли бесчисленное множество попыток внедрить электронную систему выплат по огромной и запутанной системе расчетных листов. После неудачной попытки под номером 823 руководство выбросило белый флаг и попросило Грейс вернуться на службу — всего на шесть месяцев, чтобы покончить с этим кошмаром. Грейс вернулась на флот, решила проблему и больше не оставляла ВМС. Она еще много лет служила на флоте и выступала с лекциями. В 1973 году Грейс вышла в отставку в чине капитана.

В то время Хоппер направила все усилия на выработку дополнительных неофициальных стандартов для языков программирования FORTRAN и COBOL, которые позднее были утверждены в качестве образцов Национальным бюро стандартов. Смысл этих норм сводился к следующему: системы должны строиться с учетом их фактического использования и административных возможностей. Такие системы обходятся очень дешево и не нарушают работу уже имеющегося оборудования.

В 1983 году Грейс присвоили звание командующего эскадрой. В 1985 году это звание было упразднено и ему на смену пришло звание контр-адмирала. В 1986 году, когда Грейс окончательно оставила ВМС — только ВМС, но не работу, — ей исполнилось 80 лет. Хоппер была старейшим действующим офицером, и к ней относились как к живой легенде. Тогдашний президент США Джордж Буш-старший наградил ее медалью Министерства обороны «За выдающуюся службу» (к тому времени Грейс уже имела множество наград, но ни одна из них не могла сравниться с этой). Грейс Хоппер умерла 1 января 1992 года. Она была похоронена с воинскими почестями на Арлингтонском национальном кладбище.

В числе самых необычных почестей, которых она удостоилась, стал запуск в 1996 году миноносца, названного в ее честь. Менее масштабным, но столь же необычным стало присвоение ей премии «Человек года»: в 1969 году она стала первой женщиной — лауреатом премии «Человек года» (дословно «Man of the year», что также можно перевести как «Мужчина года»), присуждаемой Ассоциацией профессионалов индустрии информационных технологий. В 1991 году, незадолго до смерти, Хоппер получила высшую американскую награду в своей области — Национальную технологическую медаль.

О любви Грейс к инновациям слагались легенды: одна из ее передовых идей, впоследствии успешно реализованная, заключалась в том, что все суда должны управляться с помощью компьютеров. Также именно Хоппер принадлежит блестящее объяснение, что такое наносекунда. Как-то ее спросили, почему передача сигнала на дальние расстояния происходит не мгновенно. В ответ Грейс разрезала старый телефонный кабель на куски длиной 30 см и вуаля — именно такое расстояние проходит свет в вакууме за одну наносекунду. Сложно придумать более наглядное объяснение.

Афиша ежегодной конференции The Grace Hopper Celebration of Women in Computing («Женщины в информационных технологиях»). Роль женщин в информационных технологиях в США до сих пор остается непростой.

* * *

COBOL

COBOL — универсальный язык программирования, позволяющий давать компьютеру инструкции непосредственно на английском (или «почти» английском) языке. COBOL, созданный в 1960 году и предназначенный для использования преимущественно в сфере бизнеса, задумывался как универсальный язык для всех компьютеров (это означает, что программу на языке COBOL можно выполнить на любой ЭВМ, и автор программы уже не является единоличным владельцем своей идеи). Название языка, по американской традиции, представляет собой акроним: COBOL означает COmmon Business-Oriented Language — общий бизнес-ориентированный язык. Впрочем, историки утверждают, что слово COBOL происходит от названия двух его основных компонентов — компилятора FLOW-MATIC Грейс Хоппер и, скорее, второстепенной программы COMTRAN компании IBM. Некоторые называют Г рейс Хоппер бабушкой COBOL.

COBOL — настолько старый, широко применяемый и, прежде всего, надежный язык, проверенный не одну тысячу раз, что улучшенные его версии используются и сегодня, спустя более чем полвека. Он по-прежнему распространен в бизнес-приложениях, хотя порой используется неявно. Доказательства популярности COBOL можно найти и в кино: робот Терминатор, сыгранный Арнольдом Шварценеггером, «разговаривает» именно на COBOL.

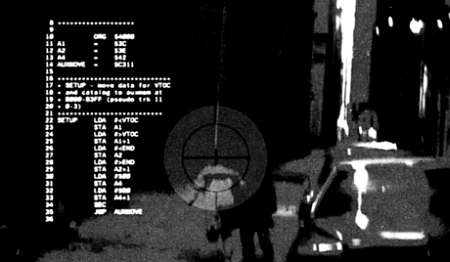
Интерфейс Терминатора, на котором видно, как робот «разговаривает» сам с собой на языке COBOL.

* * *

Джулия Боумен Робинсон (1919–1985)

Многие простые граждане США гордятся своей страной. Конечно, они не имеют в виду, что другие страны не заслуживают этой гордости, и все же часто испытывают перед их жителями некоторое чувство превосходства. Впрочем, некоторые американцы никак не могут смириться с тем, что решение десятой проблемы Гильберта — чисто математической задачи, лишенной какой бы то ни было патриотической подоплеки — принадлежит не Джулии Робинсон, блестящей американской женщине-математику, посвятившей этой проблеме несколько десятилетий. Взяв за основу крайне важные ее работы и остроумно применив известные всем числа Фибоначчи, решение проблемы нашел молодой 22-летний советский математик Юрий Матиясевич, которого отделяли от Джулии Робинсон тысячи километров. Джулия подошла к решению задачи очень близко, но первой финишную черту переступила не она. Несмотря на это в ряде книг, статей и газетных заметок безапелляционно заявляется, что именно Джулия разгадала эту математическую загадку. Помимо национальной гордости, есть и другие причины приписать ей достижение, которое она сама, с присущей ей скромностью, никогда своим не считала. Джулия была не просто женщиной, но лучшей и самой известной женщиной-математиком США и, возможно, — теперь мы не погрешим против истины — всей Америки. Ей вполне по силам было разгадать загадку.

Джулия Робинсон в мае 1941 года.

Хроника предначертанного пути

Джулии Боумен при рождении было суждено стать математиком. Ее старшая сестра, которая после замужества стала именоваться Констанс Рид, прославилась не как математик, а как автор биографий математиков. Ее книгу о Гильберте специалисты считают образцовой. По счастливой случайности, сестра Констанс также стала знаменитой. Она достойна отдельной биографии.

Когда Джулии было два года, ее мать умерла, и отец, Ральф, на время отправил Джулию и Констанс к бабушке, в Аризонскую пустыню, а сам начал жизнь с чистого листа. Он женился второй раз, оставил свой машиностроительный бизнес, вложил солидные сбережения, переехал в Калифорнию по желанию второй жены, которая хотела дать девочкам хорошее образование, и посвятил себя семье.

В то время Джулия не отличалась быстрым умом. В девять лет она целый год проболела скарлатиной. После того как вся семья прошла карантин, они отпраздновали выздоровление дочери походом в кино на первый звуковой фильм. Но радость была преждевременной — одним из осложнений этого страшного в те годы заболевания стала острая ревматическая лихорадка. Из-за болезни Джулии пришлось провести в постели много месяцев, а затем еще два года она не могла регулярно ходить в школу. Ревматическая лихорадка обычно поражает сердечные клапаны, и у Джулии развилась хроническая болезнь сердца.

Наконец девочка оправилась от болезней, и родители наняли ей репетитора, чтобы наверстать упущенное. Джулия справилась блестяще — четырехлетнюю программу она освоила за год. Похоже, именно в те годы в ней начала просыпаться тяга к математике. Репетитор показала, что десятичные знаки ?2 ведут себя непредсказуемым образом, что характерно для так называемых иррациональных чисел: если знаки периодических дробей с определенной позиции повторяются, то в записи ?2 никаких повторов не наблюдается. Это показалось Джулии столь удивительным, что она провела остаток дня за вычислением все новых и новых знаков этого числа. С того дня числа стали друзьями Джулии.

Вернувшись в класс, она устремилась к знаниям и вскоре оказалась лучшей ученицей по точным наукам. К окончанию школы родители преподнесли ей царский для тех времен подарок — ее первую логарифмическую линейку, которую Джулия шутливо называла Slippy («скользкая»). Все были согласны с тем, что девочке следовало стать преподавателем математики, а для этого требовалось окончить колледж в Сан-Диего (в те времена он еще не назывался Калифорнийским университетом в Сан-Диего). Но Джулия не хотела ограничиться преподаванием и решила сделать математику своим призванием. По всей видимости, на ее решение повлияла биографическая книга под названием «Творцы математики» Эрика Темпла Белла. Следует отметить, что эта книга действительно написана очень увлекательно и способна вдохновить любого.

В судьбу Джулии вмешался кризис 1929 года, ставший причиной трагедии: отцовские сбережения растаяли, и Ральф Боумен, не в силах пережить потрясение, покончил с собой. Положение семьи пошатнулось, но, благодаря помощи тети, семья осталась на плаву, и Джулия продолжила учебу. На все личные расходы она получала ровно 12 долларов в семестр.

Благодаря тяге к знаниям и трудолюбию, а также финансовой поддержке сестры Констанс, которая к тому времени уже преподавала, Джулия прослушала несколько курсов в Калифорнийском университете в Беркли. Дальнейшая учеба не особенно помогала в поисках работы: работодатели спрашивали Джулию не о математике, а о том, как быстро она печатает на машинке. В Беркли Джулия влюбилась одновременно в красоту высшей математики и в очаровательный голос одного из преподавателей — юного Рафаэля Робинсона (1911–1955). В университете девушка узнала, что была прекрасным лебедем среди гадких утят. Именно там она впервые почувствовала себя по-настоящему счастливой. Незадолго до того как мир содрогнулся от нападения на Пёрл-Харбор, Джулия и Рафаэль поженились.

Джулия Боумен выходит замуж

Согласно университетским правилам, Джулия не могла преподавать математику на той же кафедре, что и ее муж. К счастью, Ежи Нейман (1894–1981) пригласил ее заняться статистикой в лабораторию секретных военных проектов. Джулию всегда привлекала эта сфера, особенно после того как она познакомилась с впечатляющей бейсбольной статистикой. И все же статистика не была истинной страстью Джулии — ее больше привлекала рискованная жизнь профессионального математика. Впрочем, к новой работе она отнеслась со всей серьезностью. Как-то раз Джулию попросили описать, как проходит ее обычная неделя. Она ответила: «Понедельник: попытаться доказать теорему. Вторник: попытаться доказать теорему. Среда: попытаться доказать теорему. Четверг: попытаться доказать теорему. Пятница: теорема оказалась неверной».

Джулия с мужем Рафаэлем Робинсоном.

Джулия и Рафаэль хотели завести ребенка, и Джулия стала уделять математике меньше времени, готовясь стать матерью. Она забеременела, но, к несчастью, потеряла плод. Возможно, тем самым она спасла себе жизнь: врач обнаружил в митральном клапане Джулии рубцовую ткань и сообщил супругам, что ее слабое сердце не выдержит еще одной беременности. Более того, доктор признался мачехе Джулии, что если ее падчерица доживет до 40 лет, это будет чудом. Молодая пара была вынуждена остаться бездетной. Чтобы справиться с депрессией, Джулия при поддержке Рафаэля с головой ушла в математику.

В 1946 году она получила степень доктора под руководством выдающегося математика Альфреда Тарского (1902–1983), защитив диссертацию о проблемах разрешимости в арифметике рациональных чисел (Definability and Decision Problems in Arithmetic). Джулия столкнулась с подобными проблемами впервые, и, по всей видимости, они произвели на нее неизгладимое впечатление. Именно Тарский первым заговорил с подопечной о диофантовых уравнениях.

За исключением всего двух важных статей, все математические труды Джулии Робинсон касались десятой проблемы Гильберта (о ней мы более подробно поговорим далее) и проблем разрешимости. Первая из этих двух статей (A Note on Exact Sequential Analysis) была посвящена аналитико-статистической задаче и написана в период совместной работы с Нейманом. Во второй статье, опубликованной в 1951 году, во время короткого периода работы в корпорации RAND (ведущем американском мозговом центре), рассматривалось решение проблемы равновесия Нэша в теории игр, в то время находившейся на пике популярности, называлась эта работа «Итеративный метод решения игр» (An Iterative Method of Solving a Game).

Как видите, Джулия Робинсон и диофантовы уравнения были словно созданы друг для друга.

Диофантово уравнение — это уравнение с одной или несколькими неизвестными с целыми коэффициентами, решения которого принадлежат множеству целых чисел . Эти уравнения названы в честь древнегреческого математика Диофанта Александрийского (ок. 200–214 — ок. 284–298), который посвятил им целый трактат — «Арифметику». Примером диофантового уравнения является уравнение с тремя неизвестными

х² + у² = z².

Как вы знаете, это уравнение выражает теорему Пифагора, и еще с глубокой древности известно, что оно имеет бесконечно много решений. В параметрическом виде решениями этого уравнения являются тройки чисел вида:

х = m² — n²,

у = 2mn,

z = m² + n²,

где m и n — целые числа. Такие тройки чисел называются пифагоровыми и известны уже много веков. Намного интереснее выглядят тройки ненулевых чисел х, у, z, когда выполняется условие

хⁿ + уⁿ = zⁿ, n > 2.

В этом случае указанное диофантово уравнение не имеет решений. Так формулируется знаменитая теорема Ферма, доказанная в 1995 году. Десятая проблема Гильберта была не столь «простой» и звучала принципиально иначе: в ней требовалось найти алгоритм, позволяющий определить, имеет ли решения произвольное диофантово уравнение. К счастью, сегодня мы знаем, что такого алгоритма не существует. Для решения десятой проблемы Гильберта потребовалось не 300 лет, как на доказательство теоремы Ферма, но целых 70, а также ряд блестящих идей.

В 1961 году, когда Джулии было чуть за 40, прогнозы врачей подтвердились: ей потребовалась операция на сердце. К счастью, кардиохирургия в те годы была уже достаточно развитой, и лечение прошло успешно. Однако сердце Джулии было слишком слабым, и ей нельзя было перенапрягаться. В результате, когда в 1976 году она стала профессором Калифорнийского университета в Беркли, руководству пришлось согласиться с тем, что преподавать Джулия будет всего на четверть ставки. После операции Джулии порекомендовали езду на велосипеде, и она отдалась этому занятию с такой страстью, что стала покупать велосипеды один за другим, стремясь найти самый легкий и управляемый. Ее муж жаловался: «Другие жены покупают пальто или бриллиантовые браслеты, а моя жена покупает велосипеды».

В 1984 году у Джулии Робинсон обнаружили лейкемию. Благодаря лечению болезнь отступила, но ненадолго: исследовательница умерла в 1985 году.

Десятая проблема Гильберта

На математическом конгрессе 1900 года Давид Гильберт, ведущий математик мира, представил список из 23 нерешенных задач. Решение этих задач, по его мнению, означало бы существенное развитие математики. Гильберт предполагал (для тех времен такая точка зрения была вполне логичной), что любая проблема имеет решение, и рано или поздно все 23 его проблемы будут решены. Сегодня нам известно, что Гильберт ошибался: спустя много лет Курт Гёдель доказал, что существуют задачи, парадоксальным образом не имеющие решения. Между прочим, одной из подобных неразрешимых проблем оказалась континуум-гипотеза — первая же проблема в списке Гильберта. Вне зависимости от того, будем мы считать континуум-гипотезу истинной или ложной, в рамках формальной логики мы никогда не придем к какому-либо противоречию.

Диофантовыми называются полиномиальные уравнения вида

Р(х₁, х₂, …, х_n) = 0

с решениями и коэффициентами на множестве . Проблема Гильберта под номером 10 звучала так: существует ли алгоритм или метод, позволяющий определить, имеет ли решения произвольное диофантово уравнение? В конце концов в 1970 году было доказано, что такого алгоритма не существует. Десятая проблема Гильберта допускает бесконечное множество случаев. Известны подмножества случаев, для которых искомый спасительный алгоритм существует, однако в задаче требуется найти универсальный алгоритм для всех возможных случаев. К примеру, алгоритм Евклида позволяет решить диофантовы уравнения вида

ax ± by = с,

но не уравнения произвольного вида (указанные уравнения имеют решения тогда и только тогда, когда НОД (а, Ь) является делителем с). Путь к решению десятой проблемы Гильберта непрост, и многие не сразу поймут его. Но мы все же попытаемся описать ее решение, пусть и очень поверхностно.

В 1950 году Джулия Робинсон, применив некоторые свойства уравнения Пелля, не смогла доказать, что определенное числовое множество, которое мы обозначим JR в честь Джулии Робинсон (его нельзя построить, но можно определить в терминах общей арифметики), является диофантовым (см. врезку, посвященную Алану Тьюрингу), но не вычислимым. Множество JR обладало некоторыми интересными свойствами — в частности, его элементы возрастали по экспоненциальному закону.

Доказать указанное свойство не удалось, однако эта гипотеза с высокой вероятностью считалась истинной. Далее будем называть эту гипотезу гипотезой JR. В 1959 году Мартин Дэвис и Хилари Патнем доказали, что при определенных условиях из гипотезы JR следует очень важный результат: любое рекурсивно перечислимое множество является диофантовым. Если выполняются начальные условия и гипотеза JR, то десятую проблему Гильберта можно считать решенной, и ответ на нее будет отрицательным.

* * *

НЕМНОГО ТЬЮРИНГА

При решении проблем разрешимости и вычислимости, а также логических задач обычно используются машины Тьюринга. Эти машины, придуманные английским ученым Аланом Тьюрингом (1912–1954), в действительности представляют собой идеальные математические абстракции вычислительных машин с бесконечной памятью. Представьте себе ящик с входным и выходным отверстиями, через которые проходит бумажная лента, разделенная на прямоугольные ячейки. В каждой ячейке записана цифра — 0 или 1. В крышке ящика есть смотровое отверстие, через которое в любой момент можно увидеть, какая цифра записана в ячейку. На каждом шаге цифру в ячейке можно заменить на 0 или 1. Аналогично, можно определить, куда следует переместить считывающее устройство на следующем шаге: влево или вправо. Новая записанная цифра и новое состояние машины зависят от текущего состояния машины, а следующий шаг (и следующее состояние) указаны в программе, записанной в управляющем устройстве. Программы различных машин Тьюринга отличаются. Прекратит ли машина работу, зависит оттого, что указано в программе. Может показаться, что от столь простого устройства не стоит ждать многого, однако потенциал машины Тьюринга огромен.

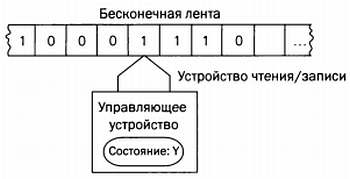
Простейшая схема работы машины Тьюринга.

Далее приведены три определения, тесно связанные с работами Джулии Робинсон и диофантовыми уравнениями. Они приводятся отдельно, так как используются в рассуждениях, самих по себе достаточно сложных.

— Перечислимое множество (по историческим причинам также называется рекурсивно перечислимым): множество целых чисел L называется перечислимым, если существует машина Тьюринга такая, что если ввести в нее целое число, она остановится на 1, если указанное число принадлежит L Если указанное целое число не принадлежит L, машина может остановиться на 0 или не остановиться никогда.

— Вычислимое множество: множество С называется вычислимым, если существует программа машины Тьюринга такая, что для любого введенного целого числа машина останавливается на 1, если это число принадлежит С, в противном случае — на 0. Чуть менее понятное, но эквивалентное определение вычислимого множества таково: множество С называется вычислимым тогда и только тогда, когда С и его дополнение С^? являются перечислимыми. Очевидно, что любое вычислимое множество является перечислимым, но не наоборот.

— Диофантово множество: множество целых чисел D называется диофантовым, если его можно определить с помощью многочлена Р (x₁, x₂, x_t) от переменных d, t, x₁, x₂…., x_t >= 1 с целыми коэффициентами такого, что Р обращается в ноль при присвоении целых значений x₁, x₂…., x_t тогда и только тогда, когда d равно одному из элементов множества D.

Алан Тьюринг.

* * *

Всего годом позже в игру вступила Джулия Робинсон: ей удалось упростить задачу и устранить неудобные начальные условия, описанные Дэвис и Патнем. Ситуация была такова: если возможно множество вида JR, то десятая проблема Гильберта будет решена. Достаточно найти диофантово уравнение с определенными решениями, возрастающими экспоненциально, но это уравнение ускользало от математиков. Открытие было совершено в 1970 году, спустя почти 30 лет поисков. Юный математик Юрий Матиясевич из Советского Союза представил колоссальную систему диофантовых уравнений:

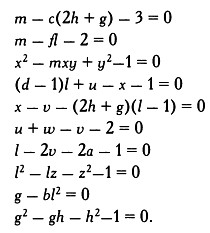
Если мы возведем обе части всех этих уравнений в квадрат и сложим их почленно, то получим одно уравнение, которое будет иметь те же решения на множестве натуральных чисел, что и вся система. Полученное уравнение будет удовлетворять необходимым начальным условиям.

Матиясевич получил приведенные выше десять уравнений не случайно: он использовал в работе весьма остроумные методы. Ключевую идею математик заимствовал из теоремы, доказанной в 1942 году и затерянной на страницах третьего издания старенькой книжечки под названием «Числа Фибоначчи» советского математика Николая Воробьева. Для десяти приведенных выше уравнений выполняется равенство v = F_2 м, где F_i — i-e число Фибоначчи. Интересно, что эта теорема приводится только в третьем издании книги Воробьева и отсутствует в первых двух.

Условия, которым удовлетворяют решения уравнения Матиясевича, согласуются с условиями гипотезы JR. Следовательно, мы можем говорить уже не о гипотезе, а о доказанной теореме. Неуловимое множество JR было найдено, следовательно, десятая проблема Гильберта решена: искомого чудесного алгоритма не существует.

Таким образом, путем невероятных умственных усилий удалось доказать: не существует алгоритма, позволяющего определить, имеет ли решение произвольное диофантово уравнение. Всегда найдется уравнение, перед которым спасует любой алгоритм.

Решение десятой проблемы Гильберта основано на тонком различии между перечислимым и вычислимым множеством. Матиясевич, Робинсон, Дэвис и Патнем доказали прекрасный и удивительный результат:

Множество является перечислимым (рекурсивно перечислимым) тогда и только тогда, когда оно является диофантовым.

Однако суть проблемы Гильберта заключается в том, что не все перечислимые множества являются вычислимыми. Достаточно найти одно-единственное перечислимое, но не вычислимое множество, чтобы дело приняло совершенно иной оборот. Это множество будет диофантовым, но соответствующее диофантово уравнение нельзя будет решить никаким алгоритмом.

* * *

УРАВНЕНИЕ ПЕЛЛЯ

Английский математик Джон Пелль (1611–1685) вошел в историю благодаря уравнению, носящему его имя:

x² — d(y + 1)² = 1.

Это уравнение имеет целые решения тогда и только тогда, когда d не является квадратом. Согласно определениям, приведенным во врезке, посвященной машине Тьюринга, множество чисел, которые не являются квадратами, D = {2, 3, 5, 6, 7, 8, 10…}, является диофантовым.

* * *

Жизнь после десятой проблемы

На день рождения Джулия получила торт с зажженными свечками, задула их и загадала свое обычное желание: дожить до того дня, когда будет найдено решение проклятой проблемы под номером 10, и не важно, кто его найдет и каким будет ответ — положительным или отрицательным. Пока Джулия Робинсон ожидала решения десятой проблемы Гильберта, она успела получить множество почетных наград. Крупнейшей в денежном выражении стала стипендия фонда МакАртура, присужденная ей в 1983 году сроком на пять лет и составлявшая 60 тысяч долларов.

Джулия Робинсон, среди прочего, стала первой женщиной-математиком, принятой в члены Национальной академии наук США (1975), и первой женщиной — президентом Американского математического общества (1978). Для любого американского математика подобный пост является вершиной карьеры, однако он подразумевает определенные обязанности. Прежде чем принять назначение, Джулия посоветовалась с друзьями и родственниками и пришла к выводу, что не имеет морального права отказаться. По крайней мере, эта должность позволила ей лично встретиться на Западе, в Калгари (1982), с Юрием Матиясевичем (они познакомились еще в Советском Союзе) — советские бюрократы ревностно контролировали все заграничные командировки и выпускали советских граждан за границу очень редко и только туда, куда разрешала непредсказуемая логика партии. Во время визита Джулии в СССР математик Юрий Линник (1915–1972) заметил, что она — второй по популярности Робинсон в Советском Союзе; первым был Робинзон Крузо. Разумеется, Юрий Матиясевич и Джулия Робинсон могли переписываться и публиковать совместные статьи, ведь, как известно, в единстве сила, а расстояние во много тысяч километров не было для них преградой.

* * *

«ЗОЛОТОЙ РЕБЕНОК» ЮРИЙ МАТИЯСЕВИЧ (Р. 1947 Г.)

Нет никаких сомнений, что Юрий Матиясевич был одаренным ребенком. В 17 лет он стал победителем математической олимпиады, проходившей не где-нибудь, а в Москве. Он является почетным доктором многих университетов и членом различных академий наук, однако для математиков все эти регалии не имеют особого значения. Для них важно, что Матиясевич внес основной вклад в решение десятой проблемы Гильберта, в теории графов его именем назван полином, а его число Эрдёша равно 2. Матиясевич заинтересовался десятой проблемой Гильберта в 1965 году, в 18 лет, спустя всего год после поступления в университет.

В 22 года он нашел ее решение, что стало большим событием в мире математики. Джулия Робинсон писала в письме Матиясевичу: «Теперь, когда я знаю, что это правда, все это кажется мне прекрасным и удивительным. Если тебе в самом деле всего 22 года, мне доставляет особое удовольствие думать, что когда я сформулировала свою гипотезу, ты был еще ребенком, и мне следовало лишь дождаться, пока ты подрастешь».

Юрий Матиясевич в 1969 году, когда он нашел решение десятой проблемы Гильберта.

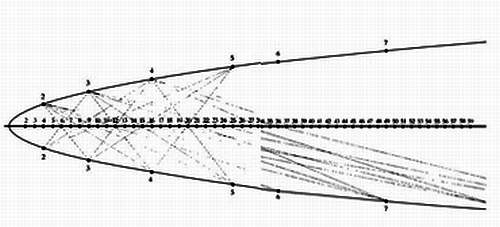
Представить себе ход мыслей Матиясевича непросто. Приведем всего один элементарный пример, который Юрий Матиясевич предложил в юности, когда ему было всего 24 года, вместе с Сергеем Стечкиным (1920–1995). Постройте параболу так, как показано на иллюстрации. Сделать это очень просто, но на всякий случай укажем, что эта парабола описывается уравнением у = х². Обозначьте на ней точки с ординатами 2, 3, 4, 5, 6 и так далее. Соедините верхние точки с нижними.

Что общего будет у всех точек, отмеченных на горизонтальной оси? Их координатами будут простые числа. Через эти точки не проходит ни одна прямая. Это построение, которое можно назвать математической игрой, называется решетом Матиясевича — Стечкина и доступно любому старшекласснику, но у всякого любителя математики при его виде перехватит дыхание. Таков Юрий Матиясевич.

* * *

Скажем несколько слов о менее известной грани личности Джулии Робинсон — о Джулии Робинсон как о политике. Она была дальней родственницей Эдлая Стивенсона (он был двоюродным братом ее мужа). Их взгляды во многом совпадали, и в 1950 году Джулия вышла на политическую сцену: она оставила математику и присоединилась к избирательной кампании Стивенсона. Когда Эйзенхауэр одержал над ним победу (причем дважды), Джулия, должно быть, испытала разочарование, а математики, занимавшиеся десятой проблемой Гильберта, напротив, вздохнули с облегчением. Как бы то ни было, Джулия Робинсон много лет была членом демократической партии.

Напоследок заметим: Джулия Робинсон всегда была сторонницей свободного доступа к знаниям и равных возможностей для всех — и мужчин, и женщин.