ГЛАВА 4 Предвестник современной науки

ГЛАВА 4 Предвестник современной науки

Три закона Кеплера были огромным вкладом в современную астрономию. Первоначально они применялись лишь к планетам, но сегодня сфера их действия распространяется на все звезды. Существует вероятность того, что во внешних частях галактик третий закон не выполняется: как предполагают, галактики погружены в темную материю. Проследим за рождением одной из самых впечатляющих гипотез современной науки о Вселенной – гипотезы о существовании темной материи.

Судьба человека зависит не только от его воли или таланта, но и от обстоятельств его жизни. По всей видимости, это правило неприменимо к Иоганну Кеплеру, рассказ о котором мы прервали на том, что ученый оказался в австрийском Линце. Здесь в это время шла война, и в конце концов математик покинул город, однако удивительно, что прежде чем сделать это, Кеплер ни на минуту не прекращал исследования и продолжал работать даже тогда, когда боевые действия развернулись в его собственном доме, причем в буквальном смысле слова.

В Европе в это время распространялась Контрреформация, требовавшая изгнать всех, кто не желал исповедовать католичество, и изъять еретические книги. Свобода вероисповедания была резко ограничена, возмущенные крестьяне подняли восстание, одержали ряд побед и осадили Линц.

Иоганн Кеплер жил здесь в прекрасном доме, расположенном рядом с городской стеной, и из окон открывался вид на прилегающую равнину. Однако после начала сражений жилье Кеплеров стало идеальным местом для наблюдения за маневрами постанцев, и в доме ученого расположились военные.

Дверь жилища была распахнута днем и ночью. Стрельба велась прямо из окон спальни в любое время суток, однако несмотря на грохот и взрывы Кеплер продолжал работать…

Он мечтал скорее отпечатать свои труды, а также завершить издание Рудольфовых таблиц, но во время одного из вооруженных столкновений городская типография Линца сгорела. После этого, в 1627 году, как мы уже писали, ученому пришлось покинуть город, оставить семью в Регенсбурге, а самому отправиться в Ульм, чтобы лично контролировать печать таблиц.

После того как книга была напечатана, Кеплер задумался о том, куда же ему теперь направиться. Братья во Христе его ненавидели, а обращаться в католичество для ученого было неприемлемо. Центральную Европу охватила ожесточенная борьба кальвинистов, лютеран, католиков и сторонников других конфессий, и этой войне суждено было продлиться 30 лет. Кеплера никто не ждал, и податься ему было некуда.

Тогда ученый решил отправиться в Прагу, чтобы лично доложить императору Фердинанду II, который к тому времени сменил на троне Матиаса, о завершении миссии и вручить ему отпечатанный экземпляр Рудольфовых таблиц. Кеплер опасался, что при дворе его встретят неприязненно, ведь новый император лично распорядился изгнать из города всех, кто не был католиком.

Однако прием оказался очень любезным. Фердинанд осыпал ученого почестями и выразил ему свое искреннее уважение, однако вскоре начал мягко подталкивать его к принятию католичества. Стоит отметить, что Кеплер называл католиками приверженцев Реформации, Контрреформации, англиканцев, кальвинистов и гугенотов, а тех, кого все называли католиками, ученый считал папистами.

Он всячески сопротивлялся переходу в другую конфессию, и к этому времени уже было ясно, что его не сломить никакими угрозами о применении силы или изгнании. Оставалось взывать к разуму ученого. Кеплер всегда ценил спокойную беседу, поэтому, несмотря на религиозные противоречия, его связывали теплые, даже дружеские отношения с некоторыми иезуитами, особенно с отцом Паулем Гульдином (1577-1643). Последнему и было поручено привести ученого в католическую веру.

Гравюра Питера де Йоде Младшего, изображающая генерала Альбрехта фон Валленштейна, приютившего Кеплера с семьей в своем дворце в городке Саган.

Иоганн Кеплер, портрет кисти неизвестного автора, 1620 год.

Один из гороскопов, составленных Кеплером для Валленштейна. Этот полководец не начинал ни одного дела без консультации с астрологом.

Как это ни парадоксально, Кеплер жаждал единения всех христиан, но при этом не был согласен отказаться от своих убеждений. Вся настойчивость и увещевания отца Гульдина разбились о несокрушимую стену, а Кеплеру пришлось покинуть Прагу. Также ему было запрещено находиться на любой католической территории империи.

Верность своим убеждениям всегда считалась похвальным качеством, однако в этот раз из-за расхождений в таких вопросах, как вездесущность Христа или правила причастия, Кеплер готов был принести в жертву будущее своей семьи и свое собственное будущее. Император и друзья ученого из числа иезуитов очень долго и очень мягко пытались склонить его на свою сторону. Все это время Кеплеру было позволено занимать должность императорского и городского математика и рассчитывать на полагающееся жалование. Однако снисходительность имела свои пределы, а ученый наотрез отказывался принять католичество несмотря на то, что братья-лютеране смотрели на него с недоверием и по-прежнему отказывали в причастии.

К счастью, в Праге судьба приготовила Кеплеру счастливую встречу с Альбрехтом Валленштейном. Этот генерал, разбивший датскую и французскую армии, считался самой влиятельной фигурой при дворе. Однако знаменитый полководец был невероятно суеверным и безоговорочно полагался на предсказания астрологов. Известно, что еще в молодости Валленштейн через третье лицо заказал у Кеплера свой гороскоп и щедро заплатил за него.

По всей вероятности, полная анонимность не была соблюдена, так что ученый знал, кому он предсказывает будущее.

По мнению Валленштейна, предсказания сбылись полностью, и генерал решил взять самого известного астролога империи под свою защиту. Сам он таким образом получал возможность постоянно прибегать к советам Кеплера.

В качестве вознаграждения за свои победы Валленштейн получил от императора герцогство Саган в Силезии, примерно в 160 км к северу от Праги, куда религиозные распри пока не добрались. Генерал не придерживался ни одного из религиозных учений и вообще был человеком дела, не терпящим разглагольствований. Валленштейн предложил Кеплеру щедрое жалование, а также предоставил в его распоряжение собственную типографию. Таким образом в 1628 году семья Кеплеров обосновалась в Сагане.

Хотя в материальном смысле жаловаться ученому было не на что, однако он страдал из-за отсутствия в городе подходящей научной и культурной среды. Кеплер не понимал местного диалекта, а горожане не знали латыни. В довершение ко всему Контрреформация добралась и до Сагана, и перед учеными встали те же трудности, что и в Граце, Линце и Праге.

Здесь мы на время отвлечемся от жизни Иоганна Кеплера и вернемся к его научным изысканиям.

ЗАКОНЫ КЕПЛЕРА В СОЛНЕЧНОЙ СИСТЕМЕ

Давайте рассмотрим влияние законов Кеплера на классическое толкование астрономических явлений и на недавние исследования в области астрофизики. Начнем с некоторых любопытных наблюдений. Орбита всех планет имеет эллиптическую форму, что отражено в таблице с данными об их эксцентриситете относительно Солнца (для Луны расчеты выполнены по отношению к Земле).

В таблицу не включен Плутон, однако его эксцентриситет также очень высок (0,25). Ввиду этого в течение сидерического года, длящегося 247,7 земного года, в определенные промежутки времени Плутон оказывается ближе к Солнцу, чем Нептун, например это наблюдалось в период с 1978 по 2000 год. Эксцентриситет, или е, рассчитывается по формуле

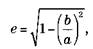
где а – это большая полуось, а b – малая полуось орбиты.

ДВИЖЕНИЯ ЛУНЫ

Орбита Луны обладает ярко выраженным эксцентриситетом, и скорость движения нашего спутника непостоянна. Это открытие было детально описано вавилонским астрономом Кидинну в IV веке до н. э. Расстояние от Земли до Луны варьируется от 406700 до 356400 км, а угловой радиус видимого диска Луны – от 29’22” до 33’31”. По этой причине скорость вращения нашего спутника также подвержена изменениям, что вызвало к жизни теорию движений Луны, на которой мы остановимся лишь вкратце.

Луна всегда обращена к Земле одной и той же стороной, поскольку период ее обращения вокруг Земли совпадает с периодом вращения вокруг собственной оси. Это явление справедливо для большинства спутников и обусловлено влиянием приливов, создающихся за счет разницы в гравитации. Другими словами, в зависимости от степени близости спутника планета притягивает его с большей или меньшей силой. В период, когда Луна находилась в менее твердом состоянии, чем сейчас, приливы вызывали большую скорость вращения на наиболее приближенных к Земле участках планеты, однако из-за трения вращение замедлялось, и влияние приливов должно было полностью исчезнуть в тот момент, когда Луна начнет обращать к Земле всегда одну и ту же сторону, то есть когда лунный день станет равен земному месяцу.

Сегодня из-за приливов океаны вращаются со скоростью, отличной от скорости движения материков, и это тормозит движение Земли. Каждые 500 лет день становится длиннее примерно на одну секунду. Хотя этот процесс проходит медленно, его необходимо учитывать при астрономических расчетах, претендующих на высокую точность.

Постепенное удлинение дня приводит к удалению от Луны в связи с эффектом сохранения кинетического момента системы Земля – Луна. Сегодня удаление составляет около 3,8 см в год.

Итак, согласно второму закону Кеплера скорость движения Луны, в отличие от скорости ее вращения, не является постоянной. Этим объясняются колебательные движения Луны, благодаря которым в определенные дни месяца мы можем увидеть небольшие участки по краям невидимой стороны Луны. То есть на самом деле мы можем наблюдать не 50, а 59 % ее поверхности.

СУТКИ НА МЕРКУРИИ

С Меркурием и его расположением по отношению к Солнцу происходит то же самое, что и с Луной по отношению к Земле. Период движения и скорость вращения планеты соотносятся не как 1:1, а как 3:2. Год на Меркурии равен 88 земным дням, что возможно рассчитать благодаря третьему закону Кеплера, а сутки – 58,65 земного дня. Из-за отливов коэффициент составляет 3/2. Год на Меркурии длится 1,5 суток, а его орбита характеризуется высоким эксцентриситетом (е = 0,206).

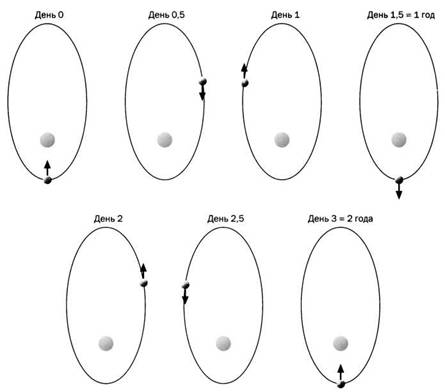
Ниже приводится длительность года и суток на Меркурии. Стрелка указывает на один из меридианов. Стоит обратить внимание на то, что этот меридиан направлен от Солнца полтора дня, к Солнцу – три дня.

Движения планеты также очень сильно выражены. В перигелии на экваторе скорость движения так высока, что сутки вполне могут стать короче года.

Вследствие этого Солнце на Меркурии восходит на востоке и движется на запад, как и на Земле, однако в полдень останавливается и начинает обратное движение на восток, затем снова останавливается и уже окончательно направляется на запад.

Меркурий поворачивается к Солнцу не всегда одной и той же стороной. В течение одного года освещена одна половина планеты, а на следующий год – ее вторая половина. Сутки длятся так долго, а расстояние от Солнца такое маленькое, что освещенная половина раскаляется, в то время как затененная – покрывается льдом. Отсутствие атмосферы не позволяет компенсировать разницу температур, и на обеих половинах планеты сохраняется экстремальное состояние. На приведенной схеме можно увидеть длительность суток и года на Меркурии.

СОЛНЦЕ

Согласно второму закону Кеплера, скорость движения Земли вокруг Солнца непостоянна. При наблюдении с Земли можно прийти к выводу о том, что угловая скорость вращения светила изменяется.

Солнечные часы не совпадают с обычными или атомными часами. Чтобы объяснить это несоответствие, давайте представим себе, что существует еще одно Солнце, которое пересекает наш небосвод с постоянной скоростью. Настоящее Солнце иногда обгоняет, а иногда отстает от воображаемого, но к концу года они подходят одновременно. Таким образом, мы можем говорить о Среднем Солнечном Времени (ССВ) и Истинном Солнечном Времени (ИСВ).

Разница между ними называется уравнением времени:

УВ = ССВ – ИСВ.

Значение уравнения времени можно узнать в специализированных астрономических изданиях или вычислить, например с помощью астрономических программ.

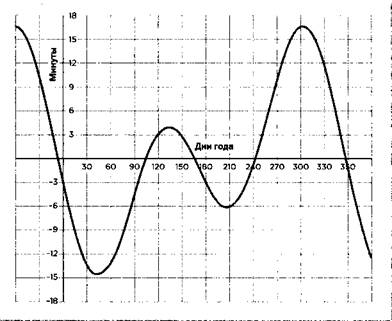
Уравнение времени, связанное с неравномерным движением Земли вокруг Солнца, следующим из второго закона Кеплера.

В англоязычных изданиях уравнение времени часто имеет инвертированный вид: ИСВ – ССВ. Уравнение времени варьируется в зависимости от времени года.

КОМЕТЫ

Кометы отличаются крайне высоким эксцентриситетом. Они проходят мимо Солнца на большой скорости, однако их апогелий находится так далеко, что по его достижении скорость комет падает практически до нуля. В результате выглядит логичной картина, согласно которой на большом удалении от Солнца кометы почти неподвижны, и в этом месте наблюдается большое их скопление. Такая гипотетическая область называется Облаком Оорта, она расположена от нас на расстоянии от 50 до 100 тысяч астрономических единиц.

Под воздействием гравитационных сил как проходящих мимо небесных тел, так и самой галактики комета начинает двигаться и увеличивать скорость по мере приближения к Солнцу, а затем, пройдя перигелий, она направляется вновь к апогелию, где ее скорость снова резко снижается. Из-за очень длинного орбитального периода за кометами невозможно проследить (подобные небесные тела называются долгопериодическими кометами). Вероятно, что многие из них вообще никогда раньше не проходили рядом с Солнцем, поэтому обнаружены лишь сегодня.

АНАЛЕММА

Если изобразить склонение Солнца (угол, на который Солнце отклоняется от небесного экватора) в зависимости от уравнения времени в каждый день года, мы получим кривую в виде восьмерки, называемую аналеммой. В силу существования уравнения времени мы наблюдаем не перемещение Солнца вверх и вниз по оси, а его смещение вправо и влево относительно истинного меридиана. На схеме дни летнего и зимнего солнцестояния располагаются, соответственно, в самой верхней и самой нижней точке аналеммы. Дни весеннего и осеннего равноденствия находятся в точках пересечения аналеммы с линей равноденствий.

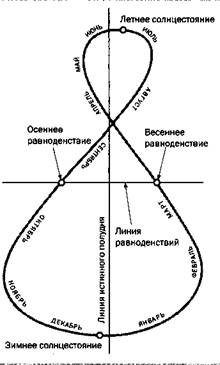
Изображение уравнения времени в форме аналеммы. За точку отсчета принят истинный меридиан.

Некоторые кометы имеют короткий орбитальный период. Мы можем их периодически наблюдать и даже предсказывать их появление (как это было с кометой Галлея). Эти небесные тела имеют большой возраст, и короткий орбитальный период связан с тем, что на их первоначальную траекторию повлияли Юпитер и Сатурн, и теперь кометы обречены на движение по орбитам с малыми гелиоцентрическими радиусами. Апогелий кометы Галлея составляет лишь 18 а.е., существуют и меньшие показатели. Эксцентриситет этой кометы равен 0,968, что существенно превосходит показатель для любой планеты, но это несоизмеримо меньше эксцентриситета долгопериодических комет.

На небесном своде, обширном и пустом, грудятся бесчисленные кометы, подобные китам в океане.

Иоганн Кеплер

Кометы, особенно короткопериодические, могут разрушаться вблизи от Солнца. Ежегодно наша планета пересекает прежнюю траекторию такой кометы, на которой находятся ее обломки, рассеянные по всей орбите. Земля проходит орбиту умершей кометы примерно в одни и те же периоды, и в это время мы наблюдаем множество падающих звезд, например, поток Леониды в ноябре и Персеиды – в августе.

ТОЧЕН ЛИ ПЕРВЫЙ ЗАКОН КЕПЛЕРА?

Ответ на этот вопрос отрицательный. Как мы знаем, многие результаты, полученные в классической физике, после открытия теории относительности были скорректированы. Вблизи от Солнца пространство и время очень искривлены. В релятивистской интерпретации планеты следуют по прямолинейным траекториям в искривленном пространственно-временном континууме, и эта характеристика усиливается рядом с Солнцем. Именно из-за этого Меркурий стал планетой, данные о которой подверглись наибольшим уточнениям. Долгота его перигелия значительно увеличена по сравнению с классическим эллипсом.

Результатом всех уточнений стала открытая траектория – эллипс, не имеющий четкого перигелия. О смещении перигелия Меркурия, которое составляет 43” за 100 лет, было известно еще до Эйнштейна. Урбен Леверье, глава Парижской обсерватории, предсказавший существование Нептуна по возмущениям на орбите Урана, объяснял смещение перигелия Меркурия влиянием планеты, которая время от времени появляется на его орбите. Авторитет Леверье был высок, и довольно долго считалось, что такая планета, названная Вулканом, действительно существует. Ее открытие в течение нескольких десятилетий приписывалось астроному-любителю Эдмону Лескарбо (1814-1894).

Однако данные Лескарбо и других наблюдателей не согласовывались ни друг с другом, ни с расчетами Леверье, и существование планеты так и не удалось подтвердить. Лишь в начале XX века поведение Меркурия было объяснено с помощью общей теории относительности Эйнштейна без введения дополнительных небесных тел.

ЧЕРНАЯ ДЫРА В ЦЕНТРЕ МЛЕЧНОГО ПУТИ

Квазары – это далекие и мощные ядра галактик, в центре которых, как полагают, находится гигантская черная дыра массой порядка 1010 массы Солнца. Однако этот признак присущ не только квазарам. Считается, что в центре обычной галактики также есть черная дыра, хотя и не столь впечатляющего размера. Такая галактика, как Млечный Путь, может иметь черную дыру массой 106 массы Солнца.

МАССА ЧЕРНОЙ ДЫРЫ

Двадцать лет назад появились подробные изображения звезд, движущихся вокруг звезды Стрелец А*, компактного радиоисточника, находящегося в центре нашей галактики. Объектом изучения группы исследователей из Института внеземной физики Общества Макса Планка стала звезда S2. Первые результаты, опубликованные в 2003 году (группа Райнера Шёделя), подтвердили наличие у нее эллиптической орбиты. К такому же выводу пришла научная группа из Университета Лос- Анджелеса. Последние данные ученых из двух исследовательских центров (Стефан Гиллисен из Института внеземной физики, 2009 год, и Андреа Гез из Университета Лос-Анджелеса, 2008 год) позволили построить орбиту согласно первому закону Кеплера. Примерная масса черной дыры составила 4 300 000 масс Солнца.

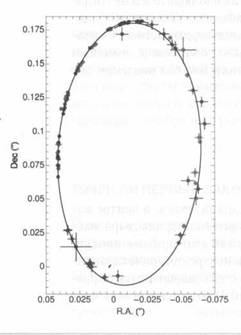
Орбита звезды S2 (в немецкой планетной номенклатуре), или S02 (в американской), пролегает в центре Млечного Пути вокруг черной дыры, равной 4,3-10 6 массы Солнца. Это изображение было опубликовано в The Astrophysical Journal. Особая благодарность Стефану Гиллисену из Американского физического общества.

Орбита звезды имеет очень высокий эксцентриситет, равный 0,87. Ее галактический перицентр составляет 17 световых лет, что в 3 раза превышает расстояние от Солнца до Плутона, а апоцентр – 10 световых лет. Максимальная скорость вращения равна 5000 км/сек, что в 200 раз превышает скорость вращения Земли вокруг Солнца.

Радиус Шварцшильда (гравитационный радиус) подобной черной дыры может составлять около 1010 м, в то время как радиус Солнца составляет порядка 7 108 м, то есть в черную дыру могут целиком уместиться некоторые звезды.

АККРЕЦИОННЫЙ ДИСК

Имеются все основания полагать, что черная дыра находится не только в центре Млечного Пути, но и в центре других галактик. Материя не поглощается ею сразу, а из-за эффекта сохранения кинетического момента скорость вращения по мере приближения к черной дыре растет – подобно тому, как вода все быстрее движется вокруг отверстия сливной трубы. Материя до поглощения черной дырой вращается вокруг нее, образуя аккреционный диск, который, предположительно, существует вокруг всех галактических черных дыр.

В аккреционном диске газ вращается вокруг черной дыры, расположенной в центре, однако, согласно третьему закону Кеплера, не все участки диска вращаются с одинаковой скоростью. Давайте мысленно разделим диск на тончайшие кольца. По третьему закону Кеплера, квадрат периода обращения этих колец пропорционален кубу расстояния до черной дыры, или же квадрат их угловой скорости w обратно пропорционален кубу расстояния r:

w?r? = константа.

Угловая скорость колец неодинакова, слои, расположенные ближе к черной дыре, будут иметь большие скорости. Это обуславливает наличие внутреннего трения и нагревания, которые наиболее высоки по мере приближения к центру и ослабевают на внешних краях диска. Внутренние слои передают часть своего момента импульса наружу, при этом они приближаются к массивному центру и, в конце концов, падают на него. Фактически траектории отдельных частиц газа имеют вид спиралей, которые медленно закручиваются. Нагревание вследствие трения приводит к выбросу излучения, что и позволяет нам наблюдать черную дыру, вернее материю, которая вращается вокруг нее.

ЗВЕЗДНАЯ МАССА

Массу Солнца можно вычислить, наблюдая за любой планетой Солнечной системы и зная расстояние от нее до Солнца и период обращения планеты. Так же мы можем рассчитать массу Земли, зная расстояние от Земли до Луны и период обращения нашего спутника, – для этого необходимо всего лишь применить закон Кеплера в интерпретации Ньютона. При помощи этого же принципа и уже указанного закона Кеплера можно рассчитать звездную массу двойных звезд, и это вычисление является практически единственным непосредственным методом вычисления звездной массы. К счастью, частью двойной системы являются многие звезды, так что к настоящему времени наработана обширная статистическая база звездных масс. Масса звезды тесно связана с ее светимостью, или световым потоком, излучаемым в секунду времени. Соотношение массы и светимости имеет следующий вид:

L аМ^х ,

где L – светимость, М – масса, х – показатель степени, равный примерно 3 или чуть больше для звезд с очень большой массой.

Подобное соотношение справедливо не только для звезд, относящихся к звездам главной последовательности, которые состоят из идеального газа, 4Н -› Не.

Двойные звезды могут быть визуальными, спектральными и фотометрическими. В случае визуально-двойных звезд при длительном изучении, например в течение нескольких лет, можно наблюдать, как обе звезды вращаются вокруг общего центра масс, двигаясь при этом по эллиптической орбите. Спектрально-двойные и фотометрические двойные звезды обычно расположены настолько близко, что расчеты крайне затруднительны, так как мы можем наблюдать лишь одну звезду, хотя мы и знаем, что на самом деле их две. В этом случае периоды обращения, как правило, гораздо меньше, и их определение не требует много времени.

Спектрально-двойные звезды можно обнаружить с помощью спектральных наблюдений в течение нескольких ночей. Излучение одного компонента такой звездной системы с определенной периодичностью смещается то в красную, то в синюю часть спектра в зависимости от того, удаляется или приближается звезда. Если спектр второго компонента демонстрирует аналогичные смещения, но в противофазе, то можно утверждать, что перед нами двойная система. Подобное поведение вызвано эффектом Доплера и движением звезды по орбите и позволяет довольно точно определить период ее обращения.

В случае фотометрических двойных звезд мы наблюдаем изменение кривой силы света, то есть отношения светового потока ко времени, из-за того, что звезды затмевают друг друга. Для наблюдения этого явления необходимо, чтобы плоскость орбиты находилась на линии видимости.

Информация, получаемая в ходе наблюдений за двойными системами, меняется в зависимости от типа наблюдения. Расчеты могут быть более или менее сложными, однако принцип остается неизменным. Не будем вдаваться в подробности формул определения массы и обратимся непосредственно к результатам. В случае визуально-двойных звезд мы наблюдаем эллипс обеих и можем рассчитать их массу:

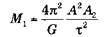
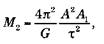
где А₁ – большая полуось звезды 1, А₂ – большая полуось звезды 2, М₁ и М₂ – их массы, А = А₁ + А₂ – расстояние между звездами, ? – период обращения. Эти уравнения выводятся непосредственно из закона Кеплера. Таким образом:

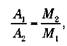
так как центр тяготения должен находиться ближе к более массивной звезде. Если 2 является планетой, М₂ << M₁ таким образом, число А₁ ничтожно мало. Это означает, что А приблизительно равно A₂ , и мы получаем закон Кеплера:

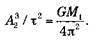
Это крайне важно для ситуаций, когда мы не видим звезды с большей массой, например в случае с черной дырой. Именно с помощью этого метода была вычислена масса черной дыры, находящейся в центре Млечного Пути.

В случае спектрально-двойных звезд можно рассчитать только массы, помноженные на наклон орбиты i, или угол между плоскостью орбиты и лучом зрения.

Если двойные звезды одновременно и спектральны, и фотометричны, могут быть получены особенно обширные данные. Возможно вычислить наклон орбиты, обе массы, а также расстояние между звездами и их радиусы.

Центр Солнца движется относительно центра тяжести Солнечной системы – барицентра. Это движение определяется двумя наиболее массивными планетами – Юпитером и Сатурном – и имеет вид почти круговых движений, согласованных с периодами обращения этих планет (около 12 и 29,5 года). Солнце удаляется от центра масс Солнечной системы на величину, приблизительно равную диаметру Солнца, и вращение происходит вокруг оси, которая, как кажется, расположена на поверхности планеты. Наблюдая за этим движением, можно сделать вывод о существовании Юпитера, хоть он и невидим.

Этот факт очень полезен при обнаружении планет, не относящихся к Солнечной системе. Боковое смещение не несет особой информационной нагрузки, так как его непросто оценить, а вот движение по эллипсу может быть прослежено с помощью эффекта Доплера. Благодаря этим методам исследования были обнаружены многочисленные планетные системы, находящиеся за пределами Солнечной.

ТЕМНАЯ МАТЕРИЯ ВСЕЛЕННОЙ

Хорошо известные нам протоны и нейтроны принадлежат к семейству частиц, называемых барионами. На современном этапе развития науки ученые полагают, что во Вселенной существуют и другие, более экзотичные компоненты, например небарионная темная материя и темная энергия. На долю барионной материи приходится всего 4 % Вселенной, на темную материю – 21 %, а темная энергия составляет – 75 %. Таким образом, материя, которую мы видим невооруженным глазом или с помощью телескопов, – малая часть того, что на самом деле наполняет Вселенную. Именно на такую мысль наводит серия наблюдений, например анизотропии космического микроволнового фона, ускорения Вселенной, кривой вращения спиральных галактик и др.

Как это связано с законами Кеплера? Темная материя изначально была обнаружена среди галактик, но одно из признанных доказательств ее существования – это вращение спиральных галактик, которое происходит слишком быстро. Если бы их тяготение было создано звездной массой и газом, оно не могло бы удерживать материю, которая движется с такой скоростью, на периферии, то есть большая центробежная сила не может быть уравновешена гравитацией, которую создает видимая материя.

Предположим, что автогравитация компенсируется центробежной силой:

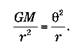
Эта формула подводит нас к третьему закону Кеплера. Мы не можем применить ее сейчас, потому что используем выражение силы тяготения, действующее для точечной центральной массы, например для Солнца, которое представляет собой практически точку в сравнении с размерами Солнечной системы. В пределах галактики материя распределена более равномерно.

Однако, анализируя ее периферию, можно считать, что вся масса сосредоточена в центральной точке. То есть предыдущая формула действительна на периферии и только на ней. Согласно ей:

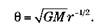
Описываемая этой формулой кривая вращения называется кривой вращения Кеплера.

Однако мы наблюдаем простое вращение, то есть на периферии скорость вращения не зависит от расстояния (см. рисунок на следующей странице). Но это означает, что галактики не повинуются третьему закону Кеплера. Вопрос о том, как это возможно, является одним из самых больших вопросов современной космологии. Если бы движение на периферии спиральных галактик подчинялось предыдущей формуле, согласно которой:

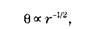
мы легко могли бы рассчитать массу галактики. Но поскольку формула не работает, узнать массу нельзя. Более того, если в первой формуле ? будет постоянной, равенство невозможно: первый член уравнения зависит от r^-2 , в то время как второй – от r^-1 .

Как можно разрешить этот парадокс, следующий из третьего закона Кеплера? Наиболее распространено следующее объяснение: в галактиках есть большое количество темной материи, которую нельзя увидеть, но которая создает гравитацию. Эта темная материя должна была бы находиться в гало (светящемся кольце) со сферическим распределением, гораздо более расширенным по сравнению с видимой материей диска спиральной галактики. При такой протяженности гало мы уже не могли бы сказать, что наблюдаем за периферией, и это означает, что кеплеровское падение происходит на гораздо больших расстояниях, где уже невозможны наблюдения (см. рисунок).

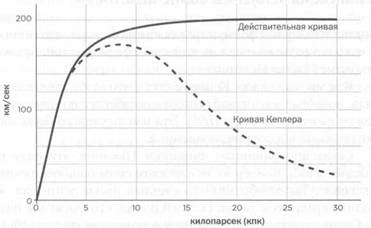
Кривая вращения типичной спиральной галактики. Для маленьких радиусов эта кривая не соответствует кеплеровскому вращению, потому что гравитация не создается точечным центральным телом. Для больших радиусов кривая должна соответствовать кеплеровскому падению, однако она не убывает, а остается постоянной. Скорее всего, это связано с существованием массивного и протяженного гало темной материи.

Масса галактики неизвестна, потому что мы не знаем, какое количество темной материи в ней содержится. Материя темного галактического гало может быть в десять раз больше видимой материи и в десять раз протяженнее.

Существуют и другие теории для объяснения кривой вращения спиральной галактики. Согласно одной из них, неверна либо формула гравитации Ньютона, либо знаменитая формула второго закона Ньютона, F = ma. В обоих случаях третий закон Кеплера не выполнялся бы, поскольку он работает в границах Солнечной системы, но несправедлив для огромных размеров и ускорений, наблюдаемых на периферии галактики. Эта теория называется MOND (Modified Newtonian Dynamics), или модифицированная ньютоновская динамика. Другие теории предполагают, что на движение галактики воздействуют и иные силы, помимо гравитационной, например магнитная.

ГРАВИТАЦИЯ КЕПЛЕРА И СОЛНЕЧНЫЕ ПЯТНА

Иоганн Кеплер не сформулировал никакой теории гравитации, однако его размышления на этот счет предвосхитили будущее открытие Исаака Ньютона.

Как мы уже знаем, Кеплер считал, что от Солнца исходит сила, подобная магнитной, которая ослабевает по мере удаления от своего источника (l/r² ). Эта мысль ученого была абсолютно новой и даже революционной.

Согласно принципам динамики Ньютона, эту силу порождает масса. Кеплер же источником силы ошибочно считал вращение. Таким образом, его светлый разум осознавал, что Солнце вращается. Когда Галилей понял, что движение пятен на Солнце подтверждает гипотезу о вращении светила, он посчитал этот факт весомым аргументом в пользу своей теории гравитации, которую можно назвать гравитацией, порожденной вращением.

Солнечные пятна и их движение впервые наблюдали, скорее всего, китайские астрономы, хотя европейцы приписывают это открытие Галилею. Кеплер спустя два года после публикации труда Галилея также наблюдал пятно. Мы уже говорили, что ученый вместо телескопа использовал перфорированный лист картона и через линзу наблюдал за перевернутым изображением, появлявшимся на экране.

Однако в описываемом случае отверстие было проделано не Кеплером. И сегодня можно наблюдать, как случайные отверстия в витражах темных готических соборов создают эффект камеры-обскуры, проецируя на пол изображение Солнца со столь высоким угловым разрешением, что без труда можно наблюдать солнечные пятна. Во время посещения великолепного кафедрального собора в Регенсбурге ученый увидел подобное изображение на стене напротив витража. Кеплер заметил движение солнечных пятен и попытался привлечь внимание других посетителей к своему невероятному открытию.

Солнце вращается, – думал Кеплер. Эта способность к вращению передается через пространство, ослабевая обратно пропорционально квадрату расстояния. Конечно, до теории гравитации Ньютона было еще очень далеко, но смелые предположения Кеплера могли повлиять на гениального британца – если тот все же сумел обнаружить их в кипах бумаг, оставшихся после смерти немецкого ученого.

Счастлив я тем, что был первым человеком, который наблюдал в этом веке пятна на Солнце.

Иоганн Кеплер после описания солнечных пятен

Можно ли, исходя из современных физических представлений, считать, что предположение Кеплера о вращении как источнике гравитации неверно? Отнюдь нет, так как искривление пространства происходит не только из-за массы, но также из-за момента и энергии, находящихся в тензоре энергии-импульса. Вращение создает момент, следовательно, искривление, а значит, и гравитацию. Безусловно, непросто найти связь между умозаключениями Кеплера и идеями Эйнштейна, но предвидение будущих открытий, свойственное великим исследователям, не может не восхищать.

В 1607 году некто наблюдал за траекторией Меркурия в непосредственной близости от Солнца. После грозы Солнце вновь появилось на небе, и его лучи проникли сквозь щели в стене дома. Мужчина взял лист белой бумаги и увидел перевернутое изображение Солнца. На нем была заметна «крошечная, почти черная точка, похожая на блоху». Рядом с мужчиной находился его друг, который также видел пятнышко. Скорее всего, это был… Меркурий! Явление редко наблюдаемое, в том числе из-за малого диаметра планеты. Меркурий пересекал солнечный диск! Эта новость была немедленно доведена до сведения императора. Помощник часовщика через отверстие в пластине также мог наблюдать точку. Он удостоверил это следующим образом:

«Генрих Штолле, младший помощник часовщика, собственноручно. Когда тучи рассеивались, было видно, что они проходят поверх точки, которая заметна на солнечном свету».

Кто же был этот мужчина, который поймал при помощи бумаги солнечный луч и сообщил императору о транзите Меркурия через солнечный диск? Конечно же, это был Иоганн Кеплер.

Однако на самом деле ученый увидел не Меркурий, а невероятных размеров солнечное пятно. Таким образом, первооткрывателем солнечных пятен в западной культуре должен считаться не Галилей, Давид Фабрициус или другой астроном, а Иоганн Кеплер, который, правда, неверно истолковал свои наблюдения.

КЕПЛЕР И ЭНТРОПИЯ

Термодинамика учит нас, что процессы имеют определенную направленность. Понятие энтропии появилось именно в рамках термодинамики и определяется как функция, характеризующая меру необратимого рассеяния энергии, или меру отклонения реального процесса от идеального. Конечно, во Вселенной возможны необратимые процессы, нарушающие всеобщее равновесие, однако их вероятность крайне мала. Согласитесь, обычно не бывает такого, чтобы камни начали летать или земля в жаркий день вдруг покрылась льдом.

Кеплер не предвосхитил появление термодинамики и не высказал никакой идеи, ценной для понимания энтропии.

Однако поскольку понятия энтропии и необратимости определяются чисто интуитивно, нередко великие мыслители формулируют суждения, важные для объяснения эволюции Вселенной. Приведем цитату из введения в книгу Кеплера «О новой звезде в созвездии Змееносца», написанного переводчиками этого труда Видалем Гонсалесом Санчесом и Николасом Гарсией Эррерой. Они изложили забавную историю из жизни Кеплера:

«Именно вчера, в тот момент, когда я устал уже от работы, но все же продолжал обдумывать мысль об атомах, летающих в воздухе, супруга позвала меня ужинать. Она поставила передо мной блюдо с овощным салатом, приправленным солью, маслом и уксусом. «А вот если бы, – задал я вопрос, – все те предметы, что я вижу вокруг себя, оловянные тарелки, листья салата, крупинки соли, капли воды и масла, кусочки резаного яйца – все это поднялось бы в воздух и полетело? Этот полет длился бы вечность, но возможно ли было, чтобы в некий момент в будущем все вновь заняло свои места в салатнице?» Моя замечательная супруга Барбара дала лучший ответ на этот вопрос. Она сказала: «Но никогда не разместились бы они с такой элегантностью и в таком идеальном порядке, как сейчас».