10
10
Известно, что де Мере предлагал Блезу другие вопросы — связанные с «умом математическим» и менее «высоким» знанием. Кавалер, как и его друг Миттон, был большим любителем азартных игр и знакомил Паскаля с проблемами, возникавшими в различных игровых ситуациях. А между тем большинство задач, оказавших существенное влияние на зарождение и первоначальное развитие теории вероятностей, связано преимущественно с азартными играми, которые давали удобные схемы для описания вероятностных явлений. Самыми распространенными азартными играми в то время были игры в кости в виде кубов с точками (от одной до шести) на каждой грани. Подсчетом количества благоприятных шансов и неблагоприятных исходов при бросании нескольких игральных костей занимались в XVI веке известные итальянские математики Кардано, Тарталья и некоторые другие ученые. Однако их вычисления не были построены на точных умозаключениях. Более полный и строгий анализ этой задачи сделал Галилей в «Рассуждении об игре в кости», в котором, в частности, решал задачу, почему при бросании трех костей в длинной серии проб цифра 11 выпала 108 раз, а цифра 12 — только 100 (по условию выигрывает тот, у кого общее количество очков превышает десять). Галилей показал, что те шесть способов, которые дают и одиннадцать и двенадцать очков, на самом деле неравноценны, так как, например, сочетание с тремя одинаковыми очками (4+4+4) встречается гораздо реже сочетания с двумя одинаковыми очками (5 + 5 + 2) и т. п. На основе более строгого учета сочетаний Галилей определил 27 вариантов выпадения цифры 11 и 25 — цифры 12, что пропорционально результатам серии. Время создания «Рассуждения...» не установлено, а опубликовано оно было лишь в XVIII веке, поэтому считается, что работа Галилея никак не повлияла на основателей теории вероятностей Паскаля и Ферма. «Наука о вероятности родилась, — пишет известный математик Пойа, — когда Паскаль и Ферма начали изучать азартные игры».
Во времена Людовика XIII азартные игры стали подлинной общественной страстью, которая заставляла скучающих аристократов и богатеющих буржуа проигрывать целые состояния. Появлялись даже подпольные игорные дома, эти «новые публичные академии, где в подражание знати говорят лишь об игре на пистоли» и где, «кроме разорения множества семейств, совершаются бесконечные злодеяния». Несмотря на королевские указы и большие штрафы (около десяти тысяч ливров), подобные дома продолжали процветать.
В этих домах и аристократических особняках возникали одинаковые затруднения, вызывавшие бурные споры. Среди них встречались и две задачи, предложенные Блезу кавалером де Мере.
Первая задача довольно проста, и ее решили одновременно Паскаль, Ферма, Роберваль и сам де Мере. Она заключалась в следующем: сколько раз надо бросать две игральные кости, чтобы шансы «прозвонить» («Звоните, дьявол умер!» — вскрикивали игроки при выигрыше), то есть в данном случае выбросить сразу две шестерки, превысили вероятность обратного результата. Различные сочетания шести граней двух костей дают в общей сложности 36 цифровых комбинаций, но только одна из них может дать двойную шестерку. Следовательно, при единократном бросании имеется один шанс «умертвить дьявола» против 35. При увеличении числа бросков в два раза соответственно увеличивается количество возможных комбинаций (362) и неблагоприятных результатов (352). Вычитая число неблагоприятных исходов из числа всех возможных комбинаций, получаем число благоприятных результатов (36n—35n). И количество бросков должно увеличиваться до тех пор, пока эта разница не превысит числа неблагоприятных результатов, что обнаруживается начиная с n = 25. Таков был результат, найденный одновременно несколькими исследователями.
Другая задача, предложенная де Мере Паскалю, гораздо сложнее. Необходимо найти справедливое распределение ставок между игроками, если игра, состоящая из ряда партий, прервана. Еще в конце XV века ее рассматривал итальянский математик Лука Пачоли, считавший, что ставки должны быть разделены пропорционально числам партий, выигранных каждым к моменту прекращения игры. Кардано справедливо возражал, что в таком случае не учитываются шансы, связанные с общим количеством партий, которые по предварительному условию необходимо было выиграть, но верного решения не дал. Блез познакомил с этой задачей Ферма и Роберваля. Последний, по словам Лейбница, не мог или не хотел понимать вероятностную проблематику и не справился с задачей, а Паскаль и Ферма нашли верный результат в своей переписке, составившей еще одну любопытную эпистолярную главу математики. 29 июля 1654 года Блез отвечает на письмо тулузца с изложением метода Ферма, переданное через Каркави (оно утеряно).
Благодаря своего корреспондента и высоко отзываясь о его методе, Блез предлагает собственный. Сначала он приводит конкретный пример, когда два игрока ставят по 32 пистоли на следующих условиях: кто первым выиграет три партии, берет обе ставки. Если предположить, что первый игрок уже выиграл две партии, а второй — одну и что играется четвертая партия, то в таком случае возможны следующие варианты: выигрыш первого игрока приносит ему 64 пистоли, а второму — ничего; выигрыш второго дает каждому по 32 пистоли (при прекращении игры). Но если они решили не проводить четвертую партию, то как разделить ставки? Первый игрок, пишет Блез, учитывая возможные результаты четвертой партии, должен сказать: «32 пистоли мне обеспечены, ибо даже в случае проигрыша я их получил бы, но остальные 32 с равными шансами могу иметь и я, и вы; таким образом, разделите их пополам и дайте мне, кроме того, еще верные 32 пистоли». Следовательно, первому игроку достанется 3/4ставки (48 пистолей), а второму — 1/4(16 пистолей). (Сравним с рассуждением Пачоли, согласно которому первый получил бы 2/3 ставки, а второй — 1/3.)
Затем Блез разбирает другой вариант раздела ставок, когда первый игрок уже выиграл две партии, а второй не выиграл ни одной. Если бы игралась третья партия, то были бы возможны два исхода: выигрыш первого игрока давал бы ему все 64 пистоли, а выигрыш второго приводил бы раздел ставок к предшествующему случаю (первому — 48, а второму — 16 пистолей). Если же решено прервать игру перед третьей партией, то первый игрок должен сказать: «При выигрыше третьей партии мне достанутся все 64 пистоли, при проигрыше ее мне законно принадлежат 48 пистолей; следовательно, дайте мне эти 48 пистолей, а остальные 16 разделим пополам, ибо у нас равные шансы выиграть их». Таким образом, первому игроку достанется 7/8 ставки (56 пистолей), а второму — 1/8 (8 пистолей).
Наконец, Блез переходит к третьему варианту разделения ставок, когда первый игрок выиграл одну партию, а второй не выиграл ни одной. Розыгрыш следующей партии мог бы дать два результата: победа первого игрока давала бы ему, как в предыдущем случае, 56 пистолей, а победа второго приводила бы к равному распределению ставки (каждому по 32 пистоли). Если же вторая партия не разыгрывается, то первый игрок должен сказать: «Дайте мне 32 уже обеспеченные пистоли, а оставшиеся от 56, то есть 24, разделим пополам. Следовательно, мне принадлежат 32 + 12 = 44 пистоли». Таким образом, первому игроку достанется 11/16 ставки, а второму — 8/16 (20 пистолей).
Паскаль делит ставку пропорционально вероятности выигрыша при различных вариантах продолжения игры и фактически пользуется теоремами сложения и умножения вероятностей, а также понятием математического ожидания. Его метод, пишет Эмиль Пикар, удивительно прост: «Составляя уравнение с конечными остатками, он изобретает один из двух аналитических методов подсчета вероятностей. Другой метод, основанный на комбинаторной теории, был дан одновременно Ферма. Такая любопытная переписка между двумя великими умами делает нас свидетелями зарождения первых принципов исчисления вероятностей».
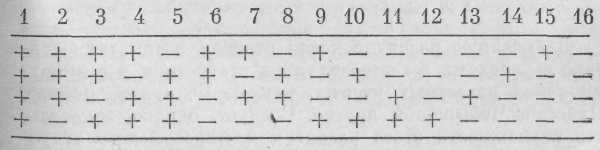
Комбинаторный метод Ферма, который в письме к Каркави от 9 августа 1654 года выражал бесконечное восхищение талантом молодого Паскаля и считал его способным довести до успешного конца любые начинания, известен из послания Блеза знаменитому тулузцу, датированного 24 августа 1654 года. В нем, в частности, приводится пример решения Ферма третьего варианта Паскалева разделения ставки, когда первый игрок выиграл одну партию, а второй не выиграл ни одной. Тулузец исходит из вероятности выигрыша всей игры: для ее окончания максимально потребовалось бы еще четыре партии, и он рассматривает возможные комбинации (их всего шестнадцать) результатов этих четырех партий, которые можно записать следующим образом (выигранные первым игроком партии обозначаются знаком +, выигранные вторым — знаком —):
Только в пяти последних исходах победителем оказывается второй игрок, одиннадцать же первых благоприятны для выигрыша его соперника. Следовательно, первый игрок должен получить 11/16 ставки, а второй — 5/16.
Полученный разными методами одинаковый результат заставляет Блеза в письме к Ферма высказать свое удо-
вольствие по поводу того, что «истина одна и та же и в Париже и в Тулузе». Хотя в процессе переписки выявились некоторые расхождения, они быстро устранились, и 27 октября 1654 года Паскаль отвечает своему корреспонденту: «Ваше последнее письмо меня полностью удовлетворило. Я восхищаюсь вашим методом раздела ставки, тем более что вполне его понимаю; оп целиком ваш, не имеет ничего общего с моим и легко приводит к той же цели. Итак, наше взаимопонимание восстановлено».
Известный историк математики Цейтен пишет, что задача де Мере позволила Паскалю и Ферма нащупать общие принципы подобного рода исследований. «Найденные дроби 11/16 и 5/16, — отмечает Цейтен, — величины, которые мы теперь называем вероятностями выигрыша А или Б; это частное от деления числа случаев, благоприятных для А или Б, на число всех возможных случаев. Таким образом, этим понятием вероятности пользовались, по существу, уже в то время, хотя ему не дано еще было четкого определения».
Более четкое и общее определение дал Гюйгенс, занявшийся вероятностными проблемами под влиянием сообщений об исследованиях Ферма и Паскаля, который в изданном в 1657 году сочинении «О расчетах в азартных играх» своеобразно (под влиянием коммерческой терминологии) сформулировал и систематически использовал понятие математического ожидания: «Если число случаев, в которых получается сумма а, равно р и число случаев, в которых получается сумма b, равно q и все случаи могут получиться одинаково легко, то стоимость моего ожидания равна (pa+qb)/(p+q)».
Дальнейшее развитие новой отрасли математики связано с успехами естествознания и статистики и с именами таких известных ученых, как Я. Бернулли, Лаплас, Пуассон, Чебышев и другие. Следует, однако, заметить, что возможности этого развития и философского углубления теории вероятностей содержались и в собственных, видимо, не осуществленных планах Паскаля. Когда в конце 1654 года Блез направил «знаменитейшей Парижской математической академии наук» послание с перечислением своих работ, он указал среди них «совершенно новый трактат о случайных комбинациях, которым подчинены азартные игры», где «колебания счастья и удачи подчиняются рассуждениям, опирающимся на справедливость и ставящим себе целью, чтобы каждый игрок неизменно получал то, что ему по праву точно причитается. Это тем в большей мере должно определяться усилиями разума, чем в меньшей мере может быть найдено из опыта. Ведь неопределенный исход явления теснее связан со случайностью, чем с законами природы. Поэтому подобные вопросы оставались нерешенными; теперь же то, что не поддавалось опыту, не может избегнуть власти разума, и мы с тем большей уверенностью подчинили их искусству математики, чтобы, овладев ими отчасти, смелее продвигаться вперед. Так математическая строгость доказательств сочетается с неопределенностью случайного и тем соединяет кажущиеся противоположности. От этой двойственности метод заимствует свое наименование, дерзко присваивая себе по праву нелепое название «математика случайного».
Однако «нелепость» и «дерзость» «математики случайного» в значительной мере устранялись тем, что в теории вероятностей, зарождавшейся из азартных игр, случай лишался своего абсолютного значения и подлинности (внезапности, неожиданности, таинственности) и превращался в реальную возможность, функционально зависимую от ожидания исполнения заранее принятых условий. Деньги, поставленные игроками на кон, писал сам Паскаль, уже не принадлежат им; но, теряя денежную собственность, игроки «приобретают право ожидания того, что случай может им дать согласно заранее оговоренным условиям».
Предварительные «правила игры» поддаются абстрактному комбинаторному исчислению и позволяют решать частные вероятностные задачи более общими методами. Так, у Паскаля имеется общее решение о разделении ставки между двумя игроками на основе изучения арифметического треугольника, названного впоследствии его именем.
«Трактат об арифметическом треугольнике» создан в период переписки с Ферма (издан в 1665 году) и тесно связан с обобщением возникших в ней комбинаторных проблем. Арифметический треугольник представляет собой числовую таблицу, верхняя строчка и первый столбец которой образованы единицами, а каждая клетка следующей строчки заполнена цифрой, получаемой от сложения чисел над данной клеткой и слева от нее. Так же образуются числа нижеследующих строк (этот процесс можно продолжать сколько угодно). Числа третьей строки назывались треугольными, четвертой — пирамидальными и т. д. Числаарифметического треугольника являются числами сочетаний, подсчитываемыми по формуле
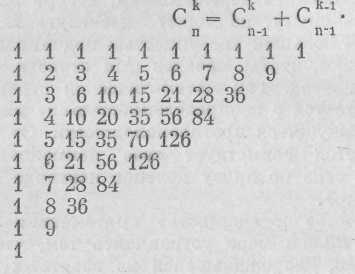
В довольно похожей форме такая таблица еще раньше была известна в странах Азии. В Европе она встречается в XVI веке у немецкого математика Штифеля и у итальянского математика Тартальи (у последнего в виде четырехугольника, стороны которого образуют последовательности фигурных чисел). Но это никак не повлияло на самостоятельность Паскаля и на значительность его вклада в комбинаторику.
В своем трактате он излагает свойства и соотношения членов разностных рядов и биноминальных коэффициентов (они расположены по диагоналям таблицы), описывает двадцать основных следствий, вытекающих из непосредственного рассмотрения арифметического треугольника, а в небольших приложениях к трактату разбирает возможности использования этого треугольника для изучения числовых порядков и сочетаний, для определения раздела ставок между игроками и степеней биномов.
Антиалгебраизм Паскаля, неприязнь к отвлеченным формулам, сказавшиеся уже в его первых математических работах, обнаруживаются и в «Трактате...», где свойства чисел хотя и выводятся в общем виде, но описательно, с конкретными доказательными примерами, без алгебраических символов. Так, например, при определении коэффициентов степеней бинома Блез не искал априорных формул для их исчисления, а записывал их друг за дружкой, переходя от низших степеней к высшим, что не позволило ему, по словам одного французского исследователя научного творчества Паскаля, сделать открытие Ньютона: «Паскалю не хватило одного росчерка пера для написания формулы, дающей коэффициент n-го порядка, получаемого при возведении бинома в степень m: он не сделал его, позволив Ньютону прославить свое имя этим вычислением».
В числе приложений к «Трактату об арифметическом треугольнике» имеется небольшая работа под названием «О суммировании числовых степеней», написанная также в 1654 году и очень важная для дальнейшего течения мысли Блеза не только в математическом отношении. В ней Паскаль дает метод подсчета степеней чисел натурального ряда, а затем заключает: «Те, кто хотя бы в малой степени разбирается в учении о неделимых, не преминут усмотреть, что можно извлечь из предыдущих результатов для определения криволинейных площадей. Эти результаты позволяют немедленно квадрировать параболы всех видов и бесконечно много других кривых.
Если мы распространим на непрерывные величины те результаты, которые найдены для чисел по методу, изложенному выше, мы сможем высказать следующие правила.
Правила, относящиеся к прогрессии натуральных чисел, начинающейся с единицы
Сумма некоторого числа линий относится к квадрату наибольшей линии, как 1 к 2.
Сумма квадратов тех же линий относится к кубу наибольшей, как 1 к 3.
Сумма их кубов относится к четвертой степени наибольшей, как 1 к 4.
Общее правило, относящееся к прогрессии натуральных чисел, начинающейся с единицы
Сумма одинаковых степеней некоторого числа линий относится к непосредственно следующей степени наибольшей из них, как единица к показателю этой степени. Я не буду останавливаться на других случаях, так как здесь не место их изучать. Достаточно того, что мною популярна сформулированы указанные выше правила. Нетрудно найти и другие, опираясь на тот принцип, что непрерывная величина не увеличивается от прибавления к ней любого числа величин низшего порядка.
Так, точки ничего не добавляют линиям, линии — поверхностям, поверхности — телам. Или (чтобы перейти к числам, как и надлежит в арифметическом трактате) первые степени ничего не дают по сравнению с квадратами, квадраты — по сравнению с кубами и кубы — по сравнению с квадратами квадратов. Так что должно пренебрегать, как нулями, количествами низшего порядка.
Я хотел прибавить эти несколько замечаний, знакомых тем, кто пользуется неделимыми, чтобы выявить всегда вызывающую восхищение связь, которую проникнутая единством природа устанавливает между предметами, по внешности весьма далекими друг от друга. Такая связь явна в этом примере, в котором мы видим, что вычисление размеров непрерывных величин связано с суммированием степеней чисел».
Это заключение представляет собой одну из самых мастерских страниц математической литературы XVII века, по ясности и выразительности изложения его можно сравнить с физическими трактатами Паскаля. Блез практически использует слово «сумма» в том значении, в каком в современной математике употребляется понятие интеграла; кроме того, сформулированное Блезом правило об отбрасывании любого числа величин низшего порядка по сравнению с величинами более высокого порядка чрезвычайно плодотворно при анализе бесконечно малых, что позволяет считать Паскаля одним из предшественников теории пределов и анализа бесконечно малых, лежащих в основе дифференциального и интегрального исчисления. Наконец, чисто математическое различение рядов непрерывных величин, будучи перенесенным в область философии, оказывается существенно важным для понимания описываемой в «Мыслях» иерархии порядков, образующих структуру бытия: порядка материи, порядка духа, порядка любви и милосердия...
1654 год чрезвычайно плодотворен для тридцатилетнего Паскаля в научном отношении. В «Послании Парижской академии» он приводит обширный аналитический перечень своих напечатанных и неопубликованных математических сочинений: «Эти работы, весьма знаменитые ученые, я преподношу вам или вам их возвращаю; в самом деле, я считаю как бы вашими те из них, которые не были бы моими, если бы я не сформировался среди вас». Паскаль, едва сам подозревая о том, «возвращал» свои труды не только в почтенно-метафорическом смысле. 1654 год стал для него и годом решающих перемен, отхода от научных проблем сформировавшей его среды (он отказывается от намерения редактировать перечисленные в «Послании...» работы и публиковать уже готовые к печати), критического переосмысления собственного образа жизни и образа жизни его светского окружения.
Результаты этого переосмысления четко видны в «Мыслях».
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКДанный текст является ознакомительным фрагментом.